Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 15.Problemas - Ex. 80

Compare a temperatura adiabática de chama do combustível propano ( C 3 H 8 ), considerando um processo de combustão com quantidade estequiométrica de ar e um processo de combustão com 50% de excesso de ar. Os reagentes estão a 25 °C e 1 atm.

Passo 1

Vamos assumir que:

Existem condições operacionais estáveis.

Ar e gases de combustão são gases ideais.

As energias cinética e potencial são desprezíveis.

Não há interações de trabalho.

A câmara de combustão é adiabática.

Passo 2

Sob condições de fluxo constante, o balanço energético E e n t - E s a í d a = Δ E s i s t e m a aplicado na câmara de combustão com Q = W = 0, temos:

∑ N R ( h ° ̄ f + h ̄ - h ° ̄ ) R = ∑ N P ( h ° ̄ f + h ̄ - h ° ̄ ) P → ∑ N P ( h ° ̄ f + h ̄ - h ° ̄ ) P = ∑ N R h ̄ ° f ,   R

uma vez que todos os reagentes estão à temperatura de referência padrão de 25 ° C. Então, para o ar estequiométrico:

C 3 H 8 + a t h ( O 2 + 3.76   N 2 ) → 3 C O 2 + 4 H 2 O + a t h + × 3.76   N 2

onde a t h é o coeficiente estequiométrico e é determinado a partir do balanço de O 2 ,

a t h = 3 + 2 = 5

Então:

C 3 H 8 + 5 ( O 2 + 3.76   N 2 ) → 3 C O 2 + 4 H 2 O + 18.8 N 2

Das tabelas:

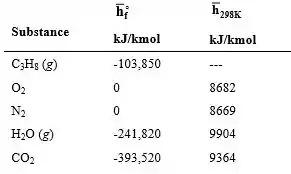
Então:

3 h ̄ C O 2 + 4 h ̄ H 2 O + 18.8 h ̄ N 2 = 2,274,680   k J

Passo 3

À 2500K:

3 h ̄ C O 2 + 4 h ̄ H 2 O + 18.8 h ̄ N 2 = 2,389,380   k J   ( M a i o r   q u e   2,274,680   k J )

À 2400K:

3 h ̄ C O 2 + 4 h ̄ H 2 O + 18.8 h ̄ N 2 = 2,334,990   k J ( M a i o r   q u e   2,274,680   k J )

À 2400K:

3 h ̄ C O 2 + 4 h ̄ H 2 O + 18.8 h ̄ N 2 = 2,280,704 k J ( M a i o r   q u e   2,274,680   k J ) )

À 2350K:

3 h ̄ C O 2 + 4 h ̄ H 2 O + 18.8 h ̄ N 2 = 2,226,580   k J ( M e n o r   q u e   2,274,680   k J ) )

Por interpolação:

T P = 2394   K =   2121   ° C

Passo 4

Quando o propano é queimado com 50% de excesso de ar, a equação da reação pode ser escrita como

C 3 H 8 + 1.5 × a t h ( O 2 + 3.76   N 2 ) → 3 C O 2 + 4 H 2 O + 0.5 × a t h O 2 + 1.5 × a t h × 3.76   N 2

onde a t h é o coeficiente estequiométrico e é determinado a partir do balanço de O 2 ,

1.5 a t h = 3 + 2 + 0.5   a t h → a t h = 5

Então,

C 3 H 8 + 7.5 ( O 2 + 3.76   N 2 ) → 3 C O 2 + 4 H 2 O + 2.5 O 2 + 28.2   N 2

Usando os valores na tabela:

3 h ̄ C O 2 + 4 h ̄ H 2 O + 2.5 h ̄ O 2 + 28.2 h ̄ N 2 = 2,377,870   k J

Passo 5

À 1800K:

3 h ̄ C O 2 + 4 h ̄ H 2 O + 2.5 h ̄ O 2 + 28.2 h ̄ N 2 = 2,333,160   k J   ( M e n o r   q u e   2,377,870   k J )

À 1840K:

3 h ̄ C O 2 + 4 h ̄ H 2 O + 2.5 h ̄ O 2 + 28.2 h ̄ N 2 = 2,392,190   k J   ( M a i o r   q u e   2,377,870   k J )

Por interpolação:

T P = 1830 K = 1557 ° C

Resposta

T P = 2394   K =   2121   ° C

T P = 1830 K = 1557 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um conjunto cilindro-pistão contém 1k g de gás metano a 100k P a e 20 ° C . O gás é comprimido reversivelmente até a pressão de 800k P a . Calcule o trabalho requerido se o processo for:a. Adiabático.
Um dispositivo cilindro-pistão contém dióxido de carbono a 1M P a e 300 ° C , com um volume de 200l . A força externa total atuando sobre o pistão é proporcional a V 3 . Esse sistema é resfriado natur
Hélio, a 20 ° C e 100k P a em um conjunto cilindro-pistão, é levado até 400K em um processo politrópico reversível com expoente n = 1,25 . Considere o hélio como um gás ideal com calor específico cons
Um dispositivo leva 2k g de amônia de 150k P a e - 20 ° C para 400k P a e 80 ° C em um processo politrópico. Determine o expoente politrópico n , o trabalho e a transferência de calor. Determine a ent
Água líquida com uma massa de 10 Kg e uma temperatura de 20 ºC é misturada com 2 Kg de gelo a uma temperatura de -5 ºC e a 1 atm de pressão até que o equilíbrio esteja alcançado. Calcule a temperatura