Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 13.Problemas - Ex. 30
Um condensador é alimentado, em regime permanente, com de vapor de um certo refrigerante. O estado termodinâmico na seção de alimentação de refrigerante é , a e, na seção de descarga, o refrigerante está no estado líquido saturado a . Calcule a taxa de transferência de calor no condensador. Admita que o vapor de refrigerante se comporta como um gás perfeito, que na saturação e que a massa molecular do refrigerante é igual a . Além disto, são conhecidas as seguintes relações para o refrigerante:
,
(a pressão está em e a temperatura em )
Passo 1
EAE GALERA, como estamos? Espero que você esteja muito bem! Se não estiver,fica firme que vai passar, me acompanha que ajudar questão resolve hehe. PRIMEIRAMENTE, vamos analisar os diagramas abaixo de Pressão por Volume e Temperatura por Entropia:
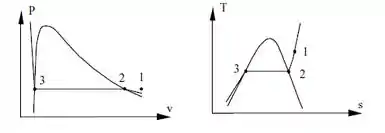
A partir desse diagrama podemos tirar as seguintes informações de cada estado:
Estado 1: ,
Estado 2: ,
Estado 3: ,
Além disso, sabemos que , usaremos as seguintes equações:
(1)
(2)
(3)
Com isso, podemos ir resolver esse problema (de uma vez por todas)
Passo 2
Primeiramente, utilizaremos a equação dada no enunciado para determinar e :
Agora, podemos passar para a equação (2) e calcular o valor de :
Com isso, podemos utilizar a equação (1) e calcular :
POR FIM, vamos utilizar a equação (3) para calcular a taxa de transferência de calor no condensador:
AÍ ESTÁ, tudo feito com sucesso! É TUDO POR HOJE, bons estudos ;)