Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 13.Problemas - Ex. 32

O particulado (partículas solidas muito pequenas) formando num processo de combustão deve ser estudado. Um dos objetivos deste estudo é o conhecimento do comportamento da pressão de sublimação desta substância em função da temperatura. Suponha que os únicos dados experimentais disponíveis são: temperatura de ebulição normal e entalpia de vaporização, h f v , na pressão normal ( 101,3   k P a ) e temperatura de fusão e entalpia de fusão, h s l , na pressão normal. A partir destas informações, desenvolva um procedimento que estime a pressão de sublimação em função da temperatura.

Passo 1

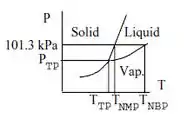
FALA AE PAE, tamo como? um dois, um dois, PIQUE DE JOGADOR, você que vem de uma sequência, chega comigo, bora pra outra. Primeiramente, vamos analisar o diagrama de Pressão por Temperatura abaixo, no qual T N B P = t e m p e r a t u a   d e   e b u l i ç ã o , T N M P = t e m p e r a t u a   d e   d e r r e t i m e n t o , T T P = p o n t o   c r í t i c o :

Assumiremos T T P = T N M P , usaremos a seguinte equação:

d P s a t d T = h f v   P s a t R T 2   (1)

Dito isto, vamos para o problema!

Passo 2

Bem, iniciaremos integrando os termos separáveis na equação (1):

d P s a t d T = h f v   P s a t R T 2

d P s a t   P s a t = d T   h f v R T 2

∫ 0.1013   M P a P T P d P s a t   P s a t = ∫ T N B P T T P d T   h f v R T 2

Os limites de integração podem ser observados no diagrama presente no enunciado, estaremos abrangendo toda aquela área para determinar a pressão de sublimação, por conta de h f v ≈ c o n s t ≈ h f v   N B P , a integral se torna:

L n P s a t ​ 0.1013 P T P ≈ h f v R ∫ T N B P T T P T - 2   d T    

L n P T P - L n 0.1013 ≈ h f v R - 1 T T N B P T T P

L n P T P 0.1013 ≈ h f v R - 1 T T P - - 1 T N B P

L n P T P 0.1013 ≈ h f v   N B P R 1 T N B P - 1 T T P

Com isso, descobrimos uma expressão que permite obter a Pressão no ponto crítico a partir da temperatura. Aplicaremos um método parecido para a Pressão de sublimação:

d P d T = h i g P R T 2

d P   P = d T   h i g R T 2

∫ P T P P S U B d P   P = ∫ T T P T d T   h i g R T 2

L n P ​ P T P P S U B ≈ h i g R ∫ T T P T T - 2   d T

L n P S U B - L n P T P ≈ h i g R - 1 T T T P T

L n P S U B P T P ≈ h i g R - 1 T - - 1 T T P

L n P S U B P T P ≈ h i g R 1 T T P - 1 T

Questão finalizada! Bons estudos e fica bem.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Amônia a –70oC é usada em uma aplicação especial com uma qualidade de 50%. Suponha que a única tabela disponível seja B.2 que desce até –50oC. Para dimensionar um tanque para conter 0,5 kg com x = 0,5
Em um motor térmico de Carnot, a adição de calor muda o fluido de trabalho de líquido saturado para vapor saturado em T, P. O processo de rejeição de calor ocorre em temperatura e pressão mais baixas
A pressão de saturação pode ser aproximada como ln Psat = A - B / T, onde A e B são constantes. Use as tabelas de vapor e determine A e B das propriedades a 25o C apenas. Use a equação para prever a p
Usando as propriedades da água no ponto triplo, desenvolva uma equação para a pressão de saturação ao longo da linha de fusão em função da temperatura.
Um recipiente com paredes duplas apresenta a cavidade formada pelas duas paredes ocupada por C O 2 a pressão e temperatura ambientes. Quando o recipiente é carregado com um líquido criogênico a 100K ,