Conforme ilustrado na Fig. P1.41, um conjunto cilindro-pistão vertical com um resistor elétrico instalado contém ar. A atmosfera exerce uma pressão de 14,7 lbf/in^2 (101,354 Pa) no topo do pistão, o qual tem uma massa de 100 lb (45,4 kg) e uma área frontal corresponde a 1 ft^2 (0,09 m^2). Conforme a corrente elétrica passa através do resistor o volume de ar aumenta, enquanto o pistão se move lentamente no cilindro. A aceleração local da gravidade é g=32,0 ft/s^2 (9,7 m/s^2). Determine a pressão do ar no conjunto cilindro-pistão, em lbf/in^2 e em psig.
Passo 1
Oii tudo bem?
Vamos lá resolver mais uma questão de termodinâmica!
Passo 2
O enunciado nos dá alguns parâmetros:
- Massa do pistão:
- Área frontal do pistão:
- Pressão atmosférica:
- Aceleração da gravidade:
Com todos os parâmetros anotados, vamos seguir para os próximos passos.
Passo 3
O diagrama mostrando a força devido a pressão atmosférica agindo no pistão, peso do pistão e força devido à pressão do ar dentro do cilindro
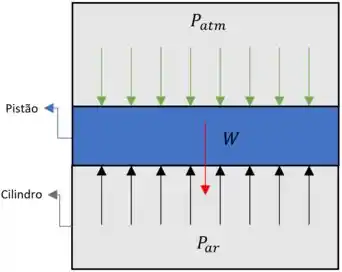
Passo 4
O peso do pistão é dado por
Passo 5
Calculando a pressão absoluta do ar no sistema usando a seguinte relação
Passo 6
Calculando a pressão manométrica do ar no sistema usando a seguinte relação