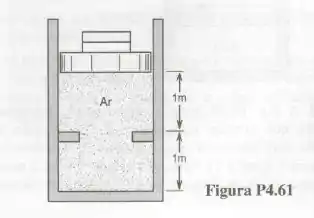
O conjunto cilindro-pistão mostrado na Fig. contém ar. Inicialmente o ar está a e . O conjunto é então resfriado até . Pergunta-se:

a) O pistão está encostado nos esbarros no estado final? Qual é a pressão final no ar?

b) Qual é o trabalho por unidade de massa realizado neste processo?

Vamos enunciar os estado:

Estado 1:

Estado 2:

a)Vamos determinar

Como temos um sistema fechado (cilindro-pistão) temos que a relação da pressão com volume e temperatura é de proporcionalidade, portanto:

Agora vamos dar uma olhadinha na imagem da questão e note que , Se considerarmos que no estado final o pistão estará encostando nos descansos.

Vamos utilizar essa relação, temos que:

Substituindo na relação de proporcionalidade:

Substituindo valores:

Temos que , logo o nosso pistão não esta apoiando nos descansos.

b)Galera o trabalho de um processo pode ser determinado pelo cálculo da área abaixo da função , por isto, vamos desenhar o diagrama:

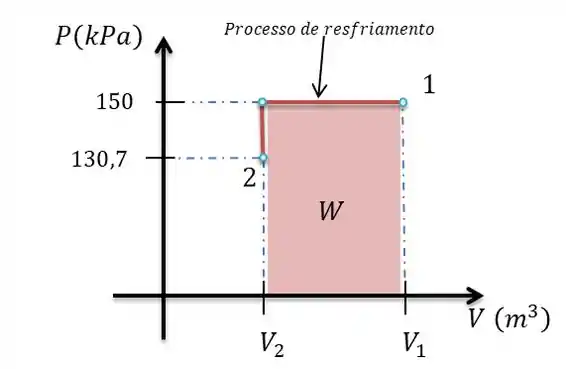
Como o pistão apenas chega em seu estado final a e ai vem o questionamento se ele esta nos descansos temos que considerar que este processo de resfriamento possui pressão constante.

Como temos um quadrado, vamos calcular a área do quadrado:

Lembrando a relação de volume, temos:

Substituindo no trabalho:

Substituindo valores:

Agora ficou claro que não temos o volume inicial, mas podemos considerar que o ar é um gás ideal e com isto resolvemos dois problemas o do volume e de que o nosso trabalho está sendo pedido em função da massa.

Temos que a equação do gás ideal é:

Olhando na tabela temos que e substituindo a pressão e temperatura, temos:

Substituindo o cálculo do volume específico no trabalho temos que o nosso resultado final fica:

É isso galera valeu.