Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 2.Problemas - Ex. 76

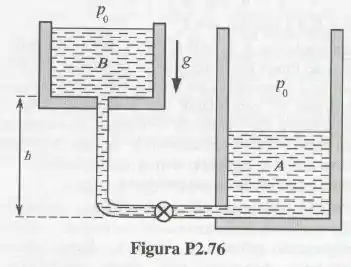
O conjunto formado pelos cilindros e tubulação com válvula mostrado na Fig. P2.76 contém água ( ρ   =   1000   k g / m 3 ). As áreas das seções transversais dos cilindros A e B são respectivamente iguais a 0.1   e   0.25   m 2 . A massa d'água no cilindro A é 100   k g enquanto a de B é 500   k g . Admitindo que h   seja igual a 1   m , calcule a pressão no fluido em cada seção da válvula. Se abrirmos a válvula e esperarmos o equilíbrio, qual será a pressão na válvula?

Passo 1

Oi pessoal, tudo certo? Vamos analisar essa questão!

Primeiramente, o exercício quer saber qual a pressão em cada seção da válvula.

A pressão na sessão esquerda é dada por:

P e s q = P 0 + ρ g h B + ρ g h

A pressão na sessão da direita será:

P d i r = P 0 + ρ g h A

Ficou claro que teremos que descobrir as alturas de água nos tanques A e B.

Podemos calcular essas informações a partir da relação de densidade. Temos que:

ρ = m V

E o volume é dado por:

V = A ⋅ h

Portanto, teremos a seguinte equação para encontrar a altura em cada tanque:

h = m A ⋅ ρ

Passo 2

Aplicando para cada situação, teremos que:

h A = m A ρ ⋅ A A

h A = 100 1000 ⋅ 0,1

h A = 1   m

Para o tanque B , temos que:

h B = m B ρ ⋅ A B

h B = 5 00 1000 ⋅ 0 , 25

h B = 2   m

Passo 3

Agora é só aplicar nas equações de pressão em cada sessão. Na sessão da esquerda a pressão será:

P e s q = P 0 + ρ g h B + ρ g h

P e s q = 101 ⋅ 10 3 + 1000 ⋅ 9,81 ⋅ 2 + 1000 ⋅ 9,81 ⋅ 1

P e s q = 130755   P a

Ou:

P e s q = 130 , 755   k P a

A pressão na válvula do lado direito será:

P d i r = P 0 + ρ g h A

P d i r = 101 ⋅ 10 3 + 1000 ⋅ 9,81 ⋅ 1

P d i r = 111135   P a

Ou:

P d i r = 111,135   k P a

Passo 4

O exercício também nos propõe calcular a pressão na válvula, se esta estivesse aberta. No caso as pressões do lado direito e esquerdo teriam que ser iguais para que houvesse o equilíbrio.

Bom... Como a pressão que encontramos do lado esquerdo é maior que do lado direito, podemos afirmar que o fluido tem direção de escoamento da esquerda para a direita.

Sendo assim, se a válvula for aberta o volume de fluido no tanque A aumentará e o volume de fluido no tanque B irá diminuir.

Podemos modelar a seguinte relação:

A A x A = A B x B

Pois o volume de água que sobe em A deve ser o mesmo que desce em B. Chamando x A da altura de água que sobe no tanque A e x B a altura de água que desce no tanque B.

Portanto:

0,1 ⋅ x A = 0,25 ⋅ x B

Logo:

x A = 2,5 x B

Passo 5

Sabendo essa relação, vamos aplicar o balanço de pressões para que o equilíbrio seja atingido. Temos que:

P 0 + ρ g h + ρ g h B - x B = P 0 + ρ g h A + x A

Simplificando, temos que:

h + h B - x B = h A + x A

Substituindo os valores conhecidos, temos que:

1 + 2 - x B = 1 + 2,5 x B

3,5 x B = 2

x B = 0,57143   m

E:

x A = 2,5 0,57143

x A = 1,4286   m

Agora é só calcular a pressão em qualquer lado, pois são iguais. Vamos calcular pelo lado direito:

P v á l v u l a = P 0 + ρ g h A + x A

P v á l v u l a = 101 ⋅ 10 3 + 1000 9,81 1 + 1,4286

P v á l v u l a = 125148,6   P a

Ou:

P v á l v u l a = 125,149   k P a

Resposta

P e s q = 130,755   k P a

P d i r = 111,135   k P a

P v á l v u l a = 125,149   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A diferença entre a pressão no corredor e na sala de um laboratório, provocada pela ação de um grande ventilador, foi medida com um manômetro de coluna d'água. Sabendo que a altura da coluna de líquid
Um conjunto cilindro - pistão apresenta diâmetro igual a 125m m e contém óleo hidráulico. A pressão atmosférica é igual a 1b a r . Determine a massa do pistão sabendo que a pressão no óleo é igual a 1
Refaça o problema anterior admitindo que o ângulo formado pelo cano do canhão e a horizontal é igual a 40g r a u s .
Refaça o problema anterior considerando que a massa específica do ar contido no reservatório é igual a 1,1k g / m 3 .
Um quilograma de oxigênio diatômico (massa molecular igual a 32 ) está contido num tanque que apresenta volume de 500L . Calcule o volume específico do oxigênio na base mássica e na molar.