Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 84
Considerando temperaturas máxima e mínima fixas, qual é o efeito da razão de pressão (a) na eficiência térmica e (b) no trabalho líquido de um ciclo Brayton simples ideal?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
No item “a” o exercício nos pergunta qual o efeito da razão de pressão na eficiência térmica, considerando temperaturas máximas e mínimas.
Bom... A eficiência térmica de um ciclo Brayton pode ser descrita, em termos da razão de pressão, por:
Vamos supor que:
Então a eficiência seria:
Agora... imaginando que este termo fosse menor e valesse agora . Teríamos que:
Então a eficiência seria:
Então podemos chegar à conclusão que quanto maior este termo menor a eficiência térmica. E, já que é uma constante, a razão de pressão que comanda este termo.
Analisando o denominador, podemos dizer que quanto maior a razão de pressão, menor este termo será e maior a eficiência:
Passo 2
Para resolver o item “b” temos que ter em mente que para um valor fixo para a temperatura na entrada da turbina, o trabalho líquido por ciclo aumenta com a razão de pressão, atinge um máximo e, em seguida, começa a diminuir, como mostra a figura abaixo:
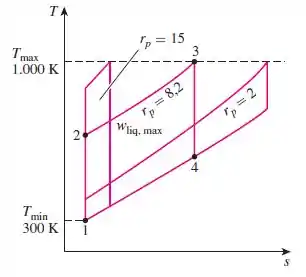
Isso acontece por que altas temperaturas na entrada da turbina podem destruir as pás levando à perda da produção de trabalho.
Resposta
O trabalho líquido por ciclo aumenta com a razão de pressão, atinge um máximo e, em seguida, começa a diminuir.