Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 11.Problemas - Ex. 16
Considerando que a válvula de expansão do é substituída por uma turbina isentrópica, determine o aumento percentual no e na taxa de remoção de calor do espaço refrigerado. Respostas:
Passo 1
Precisamos ter em mente que :
- A turbina é isotrópica
- Podemos usar as tabelas para refrigerantes ()
- O diagrama é:
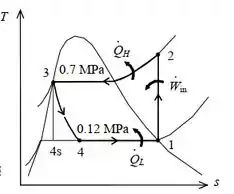
Passo 2
Se a turbina é isotrópica:
A entalpia:
Assim:
E o :
Passo 3
O aumento então será:
Resposta
Exercícios de Livros Relacionados
Numa experiência criogênica é necessário transferir calor de um espaço a 75K para um meio que apresenta temperatura igual a 180K . Projetou-se, então, uma bomba de calor, que opera em cascata (veja a
A Fig. P11.144 mostra um ciclo ideal de refrigeração associado a um ciclo motor. Os dois circuitos utilizam R - 12 como fluido de trabalho. Vapor saturado a 105 ° C sai do gerador de vapor (caldeira)
Tanto em ciclos motores, como em ciclos de refrigeração, que operam num grande intervalo de temperatura, é frequentemente vantajoso utilizar mais de um fluido do trabalho. Em ciclos de refrigeração, e
Determine a disponibilidade da água nos quatros estados do ciclo de Rankine descrito no Prob. 11.33. Admita que o reservatório a alta temperatura esteja a 500° C e que o de baixa esteja a 25 ° C . Det
Determine os fluxos de energia do condensador descrito no Prob. 11.32. Utilize seus resultados para determinar a eficiência do trocador baseada na segunda lei da termodinâmica.