A Fig. P11.144 mostra um ciclo ideal de refrigeração associado a um ciclo motor. Os dois circuitos utilizam como fluido de trabalho. Vapor saturado a sai do gerador de vapor (caldeira) e expande na turbina até a pressão do condensador. Vapor saturado a sai do evaporador e é comprimido até a pressão do condensador. A relação das vazões em massa, através dos dois circuitos, é tal que a turbina produz a potência necessária para acionar o compressor. Os escoamentos efluentes da turbina e do compressor são misturados e entram no condensador. O refrigerante na seção de saída do condensador está no estado líquido saturado a e o escoamento efluente do condensador é dividido, na proporção necessária, em duas correntes. Nestas condições, determine:
- A relação entre as vazões em massa dos circuitos de potência e de refrigeração.
- O desempenho do ciclo em função da relação
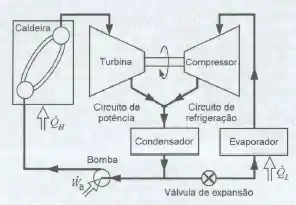
Passo 1
Olá pessoal, tudo certo com vocês? Espero que sim 😊. Vamos entender melhor essa questão?
Ela é bastante simples, basicamente é aplicação de fórmulas, nos próximos passos vocês podem relembrar dessas fórmulas. Mas antes atente-se para as imagens abaixo
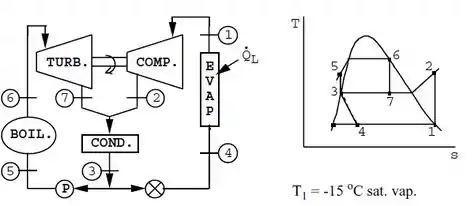
Pela tabela B.3.1, temos
Implica que,
E,
Implica que,
Logo,
Passo 2
Certo! Vamos primeiro para a turbina, note que
Como também,
Já para o compressor, tabelas computadorizadas são usadas para o devido valor de , portanto
E , implica que
Agora para a turbina mais o compressor vamos ter
Pela equação da continuidade
E pela equação da energia
Portanto
Passo 3
Agora vamos para a bomba, note que
Para o evaporador
Para a caldeira
Portanto, teremos que
Passo 4
Pronto! Finalizamos a questão 😊. Nos vemos na próxima questão. OK? Até mais.