Considere a amônia como fluido de trabalho. Construa uma tabela que apresente os valores da pressão temperatura, volume específico e título (se aplicável) para os seguintes estados: a. e ; b. e ; c. e .

a)Temos amônia como fluido sobe o estado: e .

Olhando na tabela , com a , temos as duas temperatura:

Interpolando os dados da temperatura com a pressão, podes determinar a temperatura correta.

a)Para o volume utilizaremos a fórmula do volume específico médio:

Mas para podermos aplicar esta fórmula temos que interpolar os volumes da fase líquida e vapor, para ai sim estar calculando.

Interpolando para fase líquida, temos:

Interpolando para fase de vapor, temos:

A diferença entre resultado no volume da fase de mistura, líquido e vapor ().

Volumes calculados, vamos aplicar na fórmula:

Finalizando a nossa letra (a), ficou assim:

b) o estado é: e .

Temos que olhar na tabela : temos os seguintes dados:

E

Vamos interpolar entre essas duas faixas para determinar o volume do nosso estado:

Montando o gráfico:

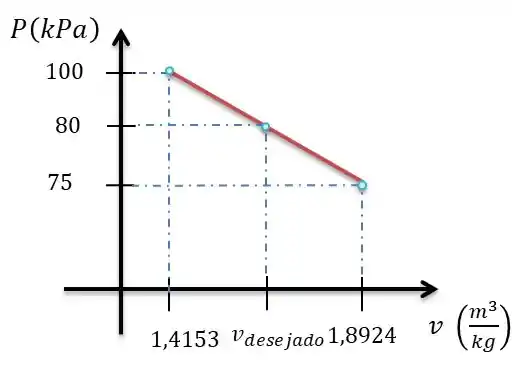
Aplicando a equação de reta, com dois pontos:

Substituindo na equação:

Para determinar o coeficiente angular, basta aplicar na equação de reta dois pontos conhecidos:

Temos que , fica:

Substituindo na o volume:

Perante o nosso título, note que o resultado final do volume é maior que o volume específico da fase de vapor da tabela para as condições de estado. Portanto, temos que nosso estado possui apenas vapor superaquecido. Estado de vapor superaquecido é bem definido e não possui título, pois, não há mistura.

A nossa letra (b), ficou:

c)Temos o estado de: e .

Olhando na tabela , com a temperatura de , vamos encontrar o volume das fases líquido e vapor.

Comparar o nosso volume de estado com os volumes sobe esta condição nós dirá se nosso estado possui mistura ou não, possui título ou não.

Olhando na tabela o volume da fase de vapor é menor que o de estado.

Portanto, temos que nosso estado possui apenas vapor superaquecido. Estado de vapor superaquecido é bem definido e não possui título, pois, não há mistura.

Vamos a interpolação, temos que determinar a pressão.

Olhando na tabela , temos os seguintes candidatos:

Repetindo o mesmo processo que fizemos para as interpolações, temos:

Substituindo na equação:

Para determinar o coeficiente angular, basta aplicar na equação de reta dois pontos conhecidos:

Temos que , fica:

Substituindo na pressão:

Nossa letra (c) ficou:

Pegando a finalização de cada letra e jogando em uma tabela: