Considere um ciclo regenerativo de refrigeração a gás que usa o hélio como fluido de trabalho. O hélio entra no compressor a 100 kPa e -10 °C e é comprimido até 300 kPa; em seguida, é resfriado até 20 °C pela água. Ele então entra no regenerador, onde é resfriado adicionalmente antes de entrar na turbina. O hélio finalmente sai do espaço refrigerado a -25 °C e entra no regenerador. Considerando que a turbina e o compressor são isentrópicos determine (a) a temperatura do hélio na entrada da turbina, (b) o coeficiente de performance do ciclo e (c) a entrada de potência líquida necessária para uma vazão mássica de 0,45 kg/s.
Passo 1
Oi pessoal, tudo bem?
Bem, para o problema de ciclo regenerativo de refrigeração a gás, podemos esboçar o diagrama T-s como:
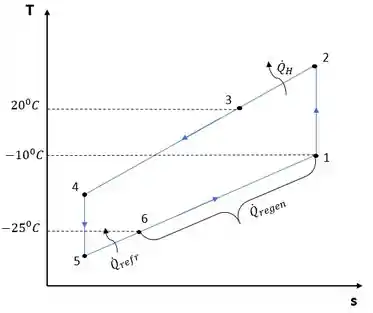
Passo 2
Bem, inicialmente o problema pede a temperatura do hélio na entrada da turbina. Realizando um balanço de energia no regenerador, temos:
Sabemos das relações isentrópicas que essa equação pode ser substituída por:
Passo 3
O COP do ciclo pode ser determinado por:
Como vimos no passo 2, aproveitando que a turbina e o compressor são isentrópicos, podemos ter a equação:
Percebemos que, as temperaturas ainda não foram encontradas. Podemos então utilizar a relação isentrópica de temperatura, assim:
Como o gás em questão é o Hélio, a partir da tabela A-2 pode ser encontrado seu respectivo calor específico à pressão constante e o , que é a razão entre os calores específicos à pressão constante e à volume constante. Então, da tabela A-2:
Portanto, a temperatura :
Da mesma forma para :
Portanto, substituindo os valores das temperaturas na equação 1, temos que:
Passo 4
A entrada de potência líquida necessária é a diferença da potência consumida pelo compressor pela potência gerada pela turbina:
Mais uma vez podemos lembrar que o compressor e a turbina são isentrópicos, então devemos dizer que:
Resposta
Portanto: