Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 3.Problemas - Ex. 60

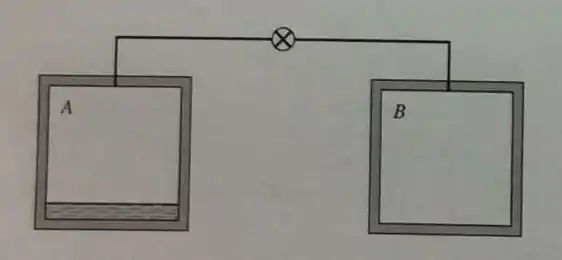
Considere dois tanques, A e B, conectados por um tubo com válvula conforme mostrado na Fig.P3.60. A capacidade de cada tanque é de 200 litros. O tanque A contém R-12 a 25°C, sendo 10% de líquido e 90% de vapor, em volume, enquanto o tanque B está evacuando. A válvula que liga os tanques é então aberta e vapor saturado sai de A até que a pressão em B se torne igual à pressão em A. Neste instante, a válvula é fechada. O processo ocorre lentamente, de modo que uma temperatura constante e uniforme de 25°C prevalece durante todo o processo. De quanto varia o título no tanque A durante o processo?

Passo 1

Fala pessoal, tudo certinho?

Mais um exerciciozinho aí pra conta!

Nós temos os seguintes dados do enunciado da questão para a substância R-12

V A = V B = V = 200   L = 0,2 m 3

T = 25 °   C = c t e

V l i q A 1 = 10 % ∙ V = 0,1 ∙ 0,2 = 0,02 m 3

V v a p A 1 = 90 % ∙ V = 0,9 ∙ 0,2 = 0,18 m 3

Nós queremos saber sobre a variação de distância

Δ x =   ?

Como a substância é R-12, nós usaremos a tabela B.3.1 a 25 ° C , obtendo

v f = 0,000763 m 3 k g

v g = 0,02685 m 3 k g

P A = 651,6   k P a

A “qualidade” de x pode ser definida como:

x = m v a p m t o t

Passo 2

Primeiro precisamos calcular a massa total (líquido e vapor) e massa de vapor:

m v a p A 1 = V v a p A 1 v g = 0,18 0,02685 = 6,704   k g

m l i q A 1 = V l i q A 1 v f = 0,02 0,000763 = 26,212   k g

Com isso, a massa total deve ser igual a

m t o t = m v a p A 1 + m l i q A 1 = 6,704 + 26,212 = 32,916   k g

Agora, nós temos que

x 1 = m v a p A 1 m t o t = 6,704 32,916 = 0,204

Depois que a válvula é aberta, o vapor saturado flui de A para B até que a pressão em B atinja aquela em A. A temperatura permaneceu em 25°C durante todo o processo. Agora no tanque B temos vapor saturado cuja massa é igual a:

m v a p B 2 = V v g = 0,2 0,02685 = 7,449   k g

A massa restante no tanque A é igual a:

m t o t A 2 = m t o t A 1 - m v a p B 2 = 32,916 - 7,449 = 25,467   k g

Passo 3

O volume específico no tanque A após o processo é igual a:

v A 2 = V m t o t A 2 = 0,2 25,467 = 0,00785 m 3 k g

Pela definição, o volume específico pode ser dado da seguinte forma:

v = 1 - x ∙ v f + x ∙ v g

Para este caso, fazendo a substituição, nós obtemos que

0,00785 = 1 - x ∙ 0,000763 + x ∙ 0,02685

Desenvolvendo um pouco mais,

0,00785 = 0,000763 + x ∙ 0,026087

Que é igual a

0,007087 = x ∙ 0,026087

Com isso,

x = 0,007087 0,026087 = 0,272

Logo,

Δ x = x - x 1 = 0,272 - 0,204 = 0,068

A qualidade no tanque A aumentou para 0,068 após o processo em comparação com a qualidade antes do processo.

Resposta

A   q u a l i d a d e   n o   t a n q u e   A   a u m e n t o u   p a r a   0,068  

Exercícios de Livros Relacionados

Um recipiente contém 1,5k g do novo fluido refrigerante R - 125 . Sabendo que o refrigerante se encontra como líquido saturado a - 20 ° C , determine o volume e a pressão interna no recipiente.
Um tanque rígido, com volume interno de 0,045m 3 , contém 2k g de acetileno a 4,3M P a . Estime a temperatura no acetileno utilizando o diagrama de compressibilidade generalizado. Observe que é necess
Um recipiente rígido contém fluido refrigerante R - 32 a - 10 ° C e x = 0,15 . Determine a pressão e o volume específico do refrigerante nesse estado.
Uma garrafa rígida, com volume de 0,1m 3 , contém butano saturado a 300K . Sabendo que o título do butano na garrafa é igual a 75 % , determine a massa de butano contida no tanque utilizando o diagram
Um tanque rígido, com volume de 0,25m 3 , contém uma substância a 2M P a e 17 ° C . Estime, utilizando o diagrama de compressibilidade generalizado, a massa contida no tanque se a substância for a) ar