Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 11.Problemas - Ex. 71
Considere uma instalação estacionária de turbina a gás que opera segundo o ciclo Brayton ideal e que fornece uma potência de a um gerador elétrico. A temperatura mínima do ciclo é e a máxima é . A pressão mínima do ciclo é e a relação entre as pressões no compressor é igual a para .
- Calcule a potência desenvolvida pela turbina e a potência que é utilizada para acionar o compressor.
- Qual é o rendimento térmico do ciclo?
Passo 1
Olá pessoal, tudo certo com vocês? Espero que sim 😊. Vamos entender melhor essa questão?
Certo! Quando menciona ciclo de Brayton, significa que:
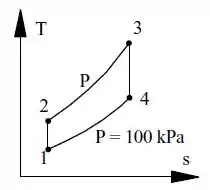
Passo 2
Agora vamos resolver usando a constante . Sabemos que, a compressão no compressor é
Assim
Passo 3
Para a expansão na turbina, temos
Assim,
Portanto, o trabalho líquido pode ser determinado como
Assim, a potência desenvolvida pela turbina e a potência utilizada para acionar o compressor é dada por:
Passo 4
No item b) pede a rendimento, então:
Passo 5
Pronto! Finalizamos a questão 😊. Nos vemos na próxima questão. OK? Até mais.