Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 11.Problemas - Ex. 60

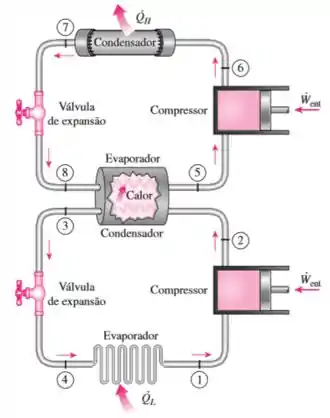
Considere um sistema de refrigeração em cascata de dois estágios operando entre os limites de pressão de 1,2   M P a e 200   k P a com o refrigerante-134a como fluido de trabalho. A rejeição de calor do ciclo inferior para o ciclo superior ocorre em um trocador de calor contracorrente e adiabático no qual a pressão dos ciclos superior e inferior correspondem a 0,4   M P a e 0,5   M P a respectivamente. Em ambos os ciclos, o refrigerante é líquido saturado, na saída do condensador, e vapor saturado, na entrada do compressor, cuja eficiência isentrópica é de 80 % . Considerando que a vazão mássica do refrigerante através do ciclo inferior é de 0,15   k g / s , determine (a) a vazão mássica do refrigerante através do ciclo superior, (b) a taxa de remoção de calor do espaço refrigerado e (c) o COP desse refrigerador.

Passo 1

Fala aí! Vamos lá resolver essa questão? Partiu!

Vamos começar visitando a tabela A-11, A-12 e A-13 para completar nossos dados:

h 1 = h g @ 200 k P a = 244,46   k J / k g s 1 = s g @ 200 k P a = 0,9377   k J / k g   .   K

h 3 = h f @ 500 k P a = 73,33   k J / k g h 4 = h 3

h 5 = h g @ 400 k P a = 255,55   k J / k g s 5 = s g @ 400 k P a = 0,9269   k J / k g   .   K

h 7 = h f @ 1200 k P a = 117,77   k J / k g h 8 = h 7

Com P 2 = 0,5   M P a → 500   k P a e s 2 = s 1 temos que:

h 2 s = 263,30   k J / k g

Partiu encontrar o h 2 usando a eficiência que nos deram no enunciado:

η C = h 2 s - h 1 h 2 - h 1

h 2 = h 1 + h 2 s - h 1 η C

h 2 = 244,46 + 263,30 - 244,46 0,80

h 2 = 268,01   k J / k g

Agora, com P 6 = 1,2   M P a → 1200   k P a e s 6 = s 5 achamos o:

h 6 s = 278,33   k J / k g

E fazemos o mesmo procedimento para achar o h 6 :

η C = h 6 s - h 5 h 6 - h 5

h 6 = h 5 + h 6 s - h 5 η C

h 6 = 255,55 + 278,33 - 255,55 0,80

h 6 = 284,02   k J / k g

Passo 2

Agora simm! Temos nossas entalpias, podemos partir para as continhas que o enunciado pediu! Na letra A, ele quer a vazão mássica através do ciclo superior, então vamos encontrar:

m A   .   h 5 - h 8 = m B   .   h 2 - h 3

m A = m B   .   h 2 - h 3 h 5 - h 8

m A = 0,15   .   268,01 - 73,33 255,55 - 117,77

m A = 0,212   k g / s

Agora vamos partir pra letra B!

Passo 3

Agora o enunciado pede a taxa de remoção de calor, vamos lá que a gente dá conta disso!

Q L = m B   .   h 1 - h 4

Q L = 0,15   .   244,46 - 73,33

Q L = 25,67   k W

Show!

Passo 4

Última letrinha agora! Nossa saideira!

O enunciado pede o COP, vamos então:

C O P = Q L W i n

Opa! Precisamos achar esse W i n , vamos, lá que a gente consegue!

W i n = m A   .   h 6 - h 5 + m B   .   h 2 - h 1  

W i n = 0,212 .   284,02 - 255,55 + 0,15   .   268,01 - 244,46

W i n = 9,566   k W

Aeee! Agora sim!

C O P = Q L W i n

C O P = 25,67 9,566

C O P = 2,68

Uhull! Conseguimos!!

Resposta

  1. m A = 0,212   k g / s

  2. Q L = 25,67   k W

  3. C O P = 2,68
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

11 – 14 Um refrigerador usa r e f r i g e r a n t e - 134 a como fluido de trabalho e opera em um ciclo ideal de refrigeração por compressão de vapor entre 0,12M P a e 0,7M P a . A vazão mássica do re
11 – 12 E Um refrigerador opera segundo o ciclo ideal de refrigeração por compressão de vapor e usa r e f r i g e r a n t e - 134 a como fluido de trabalho. O condensador opera a 300p s i a , e o evap
11 – 20 Um refrigerador comercial com r e f r i g e r a n t e - 134 a como fluido de trabalho é usado para manter o espaço refrigerado a - 30° C , rejeitando o calor dissipado para a água de resfriame
11 – 15 Repita o P r o b .11 – 14 , considerando uma pressão de condensador igual a 0,9M P a .
11 – 16 Considerando que a válvula de expansão do P r o b .11 – 14 é substituída por uma turbina isentrópica, determine o aumento percentual no C O P e na taxa de remoção de calor do espaço refrigerad