Considere um turbo compressor de um motor de combustão interna. Os gases de exaustão entram na turbina a 450 °C a uma taxa de 0,02 kg/s e saem a 400 °C. Ar entra no compressor a 70 °C e 95 kPa a uma taxa de 0,018 kg/s, saindo a 135 kPa. A eficiência mecânica entre a turbina e o compressor é de 95% (perde-se 5% do trabalho da turbina durante sua transmissão ao compressor). Considerando as propriedades do ar para os gases de exaustão, determine (a) a temperatura do ar na saída do compressor e (b) a eficiência isentrópica do compressor
Passo 1
Vamos fazer um esquema do sistema turbina-compressor, vamos considerar que a turbina tem uma eficiência interna de 100%.
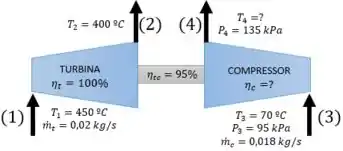
Passo 2
Primeiro, vamos começar calculando a quantidade de trabalho produzido pela turbina usando a equação:
O valor de para o ar é dado na Tabela A3, cuidado na hora de consultar a tabela, pois ela está em Kelvins. Como a turbina trabalha entre 450ºC e 400ºC, vamos pegar o na temperatura média:
Agora, vamos aplicar na equação:
Passo 3
A questão nos diz que 95% do trabalho produzido pela turbina é transferido para o compressor. Então, o trabalho do compressor é:
Passo 4
Item A)
Utilizando o trabalho absorvido pelo compressor podemos calcular a temperatura de saída:
Mas ao consultar na Tabela A3, não temos o valor do calor específico, precisaremos interpolar. Novamente, lembre-se que a Tabela A3 está em Kelvins:
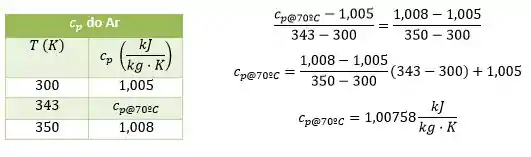
Vamos isolar a temperatura de saída:
Passo 5
Item B)
A questão nos dá a pressão de saída do compressor. Podemos utilizar as equações de processo isentrópico e descobrir a temperatura de saída em um processo ideal. Vamos aplicar a equação 7-43, lembrando que as temperaturas estão em Kelvin
Passo 6
Vamos finalizar a questão calculando a eficiência do compressor.