Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 114

A turbina a gás 7 F A produzida pela General Electric apresenta uma eficiência de 35,9 % quando em operação em ciclo simples, e uma produção de potência líquida de 159   M W . A razão de pressão é de 14,7 , e a temperatura na entrada da turbina é de 1.288   ° C . A vazão mássica na turbina é de 1.536.000   k g / h . Considerando as condições ambientais de 30   ° C e 100   k P a , determine a eficiência isentrópica da turbina e do compressor. Determine, ainda, a eficiência térmica dessa turbina a gás se for adicionado um regenerador com eficiência de 65 % .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O ciclo Brayton real com regeneração é dado por:

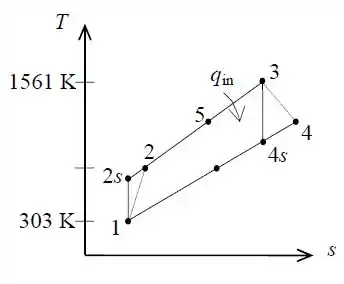
Do enunciado, temos que:

T 1 = 30 ° C + 273 = 303   K

Analisando a tabela das propriedades do gás ideal, temos que para a temperatura T 1 = 303   K , temos que:

h 1 = 303,21   k J / k g

P r 1 = 1,4356

Analisando o processo 1 → 2 s , temos que:

P r 2 s P r 1 = P 2 P 1

Portanto:

P r 2 s = 14,7 ⋅ 1,4356

P r 2 s = 21,10

Passo 2

A partir da pressão relativa P r 2 s , podemos interpolar a entalpia correspondente a partir da tabela:

h 2 s = 653,25   k J / k g

A temperatura do estado 3 será:

T 3 = 1288 ° C = 1561   K

Que nos dá:

h 3 = 1710   k J / k g

P r 3 = 712,5

A Pressão relativa do estado 4 também pode ser conseguida:

P r 4 = 1 r p P r 3 = 48,47

Para este valor podemos interpolar sua entalpia:

h 4 s = 825,23   k J / k g

Passo 3

O trabalho líquido será:

w l i q = W ˙ l i q m ˙ = 159000 1536000 ⋅ 3600   s 1   h

w l i q = 372,66   k J / k g

O calor fornecido será:

q e n t = w l i q η = 372,66 0,359 = 1038   k J / k g

Sabendo que:

q e n t = h 3 - h 2

Podemos inferir que:

h 2 = h 3 - q e n t = 672   k J / k g

Portanto:

q s a i = q e n t - w l i q

q s a i = 665,34   k J / k g

Logo:

h 4 = q s a i + h 1 = 968,55   k J / k g

A partir da tabela, para esta entalpia, temos que:

T 4 = 931,7   K

Passo 4

As eficiências isentrópicas da turbina e do compressor serão:

η t = h 3 - h 4 h 3 - h 4 s

η t = 1710 - 968,55 1710 - 825,23

η t = 83,8 %

Para o compressor, temos que:

η c = h 2 s - h 1 h 2 - h 1

η c = 653,25 - 303,21 672 - 303,21

η c = 94,9 %

Passo 5

Sabemos que a eficácia do regenerador é dada por:

ε = q r e g e n h 4 - h 2

Substituindo os valores, temos que:

q r e g e n = 0,65 ⋅ 968,55 - 672 = 192,8   k J / k g

O novo calor fornecido será:

q e n t , n o v o = q e n t - q r e g e n

q e n t , n o v o = 1038 - 192,8

q e n t , n o v o = 845,2   k J / k g

A eficiência térmica será:

η = w l i q q e n t , n o v o

η = 372,66 k J k g 845,2 k J k g

η = 44,1 %

Resposta

η t = 83,8 %

η c = 94,9 %

η = 44,1 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um ciclo Brayton ideal, ar é comprimido de 100k P a e 25 ° C para 1M P a e, em seguida, aquecido até 927 ° C antes de entrar na turbina. Sob condições do padrão a ar frio, a temperatura do ar na sa
Considere um ciclo Brayton ideal executado entre os limites de pressão de 1.200k P a e 100k P a e os limites de temperatura de 20 ° C a 1.000 ° C com argônio como fluido de trabalho. O trabalho líquid
Em um ciclo Brayton ideal com regeneração, gás argônio é comprimido de 100k P a e 25 ° C para 400k P a e, em seguida, aquecido até 1.200 ° C antes de entrar na turbina. A temperatura mais alta com a q
Em um ciclo Brayton ideal com regeneração, ar é comprimido de 80k P a e 10 ° C para 400k P a e 175 ° C , e então aquecido para 450 ° C no regenerador e depois ainda aquecido para 1.000 ° C antes de en
Por que as razões de consumo de trabalho são relativamente altas em motores de turbina a gás?