Considere uma usina de potência com ciclo combinado gás-vapor que produz uma potência líquida de 280 MW. A razão de pressão do ciclo da turbina a gás é 11. O ar entra no compressor a 300 K, e na turbina, a 1100 K. Os gases de combustão que saem da turbina a gás são usados para aquecer o vapor a 5 MPa até 350 °C em um trocador de calor. Os gases de combustão saem do trocador de calor a 420 K. Um aquecedor de água de alimentação aberto incorporado ao ciclo de vapor opera a uma pressão de 0,8 MPa. A pressão no condensador é de 10 kPa. Considerando eficiências isentrópicas de 100% para a bomba, 82% para o compressor e 86% para as turbinas a gás e a vapor, determine (a) a razão entre os fluxos de massa de ar e de vapor, (b) a taxa de fornecimento de calor necessária na câmara de combustão e (c) a eficiência térmica de ciclo combinado.
Passo 1
Tá legal, vamos primeiro ilustrar o diagrama T-s do ciclo gás-vapor, lembrando que nesse caso temos eficiência isentrópica a ser aplicada aos dispositivos, então, teremos:
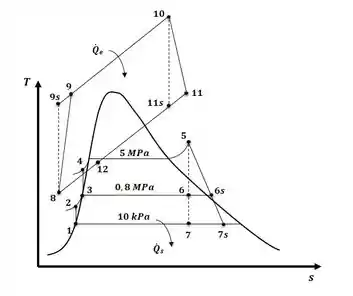
Agora, o que nós vamos fazer é trabalhar com o ciclo a gás para descobrir o valor das propriedades nos pontos de interesse. Então, com a ajuda da tabela A.17 do apêndice A, começando pelo ponto 8, temos:
Agora, da relação entre as pressões relativas entre os pontos 8 e 9, temos:
E, com esse valor, da tabela A-17, temos o valor da entalpia para a situação isentrópica:
Agora, nós sabemos que a eficiência isentrópica do compressor do ciclo superior pode ser dada por:
Com isso, podemos encontrar a entalpia real no ponto 9, então, temos:
Agora, continuando com o ponto 10, temos:
E, com isso, podemos encontrar a pressão relativa no ponto 11 através de:
Então, do apêndice A, a entalpia para o caso isentrópico no ponto 11 será:
Agora, nós sabemos que a eficiência isentrópica da turbina do ciclo superior pode ser dada por:
Então, isolando a entalpia real no ponto 11, temos:
E, por fim, podemos encontrar a entalpia no ponto 12 através da sua temperatura com o auxílio da tabela A-17, então, temos:
Passo 2
Agora nós vamos encontrar as propriedades do ciclo a vapor, de novo, com a ajuda das temperaturas e pressões e consultando as tabelas do apêndice A, então, temos:
Com isso, podemos encontrar o trabalho produzido pela bomba 1 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 1, podemos encontrar o valor da entalpia no ponto 2:
Agora, para o ponto 3, teremos:
Com isso, podemos encontrar o trabalho produzido pela bomba 2 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 2, podemos encontrar o valor da entalpia no ponto 4:
Agora, continuando com as propriedades, temos:
Com esses valores para o ponto 6, podemos encontrar seu título para o caso isentrópico através de:
Com esse valor de título, podemos encontrar a entalpia para o caso isentrópico através de:
Então, com a entalpia isentrópica, podemos aplicar a definição de eficiência isentrópica para a turbina e encontrar a entalpia real no ponto 6. Dessa forma, teremos:
Agora, nós vamos fazer a mesma análise para os pontos 5 e 7. Então, começando pelo ponto 7, temos:
Com esses valores para o ponto 7, podemos encontrar seu título para o caso isentrópico através de:
Com esse valor de título, podemos encontrar a entalpia para o caso isentrópico através de:
Então, com a entalpia isentrópica, podemos aplicar a definição de eficiência isentrópica para a turbina e encontrar a entalpia real no ponto 7. Dessa forma, teremos:
Passo 3
Agora nós vamos aplicar o equilíbrio de energia para o trocador de calor, dessa forma, teremos:
Como no nosso caso temos regime permanente, então , dessa forma, a equação se torna:
E, colocando em função das entalpias e das vazões mássicas, temos:
Então, agrupando os termos e isolando a massa de vapor, temos:
Então, substituindo os valores conhecidos, temos:
Passo 4
Agora podemos aplicar um balanço de energia para o aquecedor de água de alimentação, então, vamos ter:
Como no nosso caso temos regime permanente, então , dessa forma, a equação se torna:
E, colocando em função das entalpias e das vazões mássicas, temos:
Escrevendo em função da fração mássica , temos:
Substituindo os valores conhecidos, chegamos em:
Agora, com a fração mássica extraída da turbina do ciclo a vapor, podemos encontrar o trabalho específico produzido pela turbina nesse ciclo, então, teremos:
Substituindo os valores conhecidos, temos:
Agora, o trabalho líquido do ciclo a vapor será dado pela diferença entre o trabalho da turbina e aquele consumido pelas bombas, então, temos:
Substituindo os valores conhecidos, temos:
E, da mesma forma, o trabalho líquido para o ciclo a gás será:
Substituindo os valores conhecidos, temos:
Passo 5
Então, agora vamos calcular o trabalho líquido produzido por unidade de massa de gás, dessa forma, temos:
Substituindo os valores conhecidos, temos:
E, com isso, podemos encontrar a vazão mássica de gás através da potência produzida no ciclo, então, temos:
E então, o calor que é adicionado ao sistema pode ser encontrado pela diferença de entalpia na câmara de combustão, então, temos:
Passo 6
E, finalmente, para a letra (c), podemos encontrar a eficiência térmica do ciclo através de: