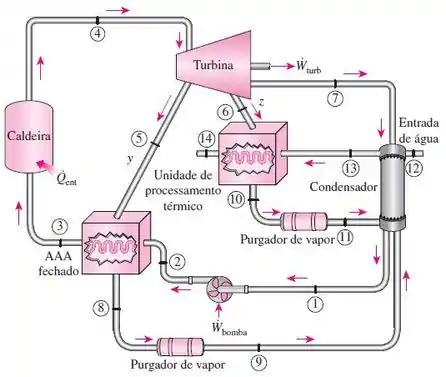
Uma grande cidade utiliza um ciclo de Rankine a vapor modificado com um aquecedor de água de alimentação fechado e uma unidade de processamento térmico para abastecer prédios próximos com água quente, usada em sistemas de aquecimento e energia elétrica, como mostrado na figura a seguir. A taxa de fluxo de vapor na turbina é de 100 kg/s. O vapor que entra na turbina é extraído a 2000 kPa, estado 5, para o aquecedor de água de alimentação. O vapor que entra na turbina é extraído a 700 kPa, estado 6, para a unidade de processamento térmico, saindo da unidade de processamento térmico como líquido saturado. Os estados para a água de alimentação da caldeira e o vapor condensado saindo do aquecedor de água de alimentação são os estados considerados normalmente ideais. A água fria do processo serve como refrigerante para o condensador e recebe o calor transferido do vapor que se condensa no condensador. A água do processo é ainda mais aquecida na unidade de processamento térmico. Use os dados fornecidos nas tabelas a seguir para determinar
(a) O diagrama T-s para o ciclo ideal,
(b) O fluxo de água de processo, em kg/s, considerando que 5% do fluxo de massa de entrada da turbina é extraído para a unidade de processamento térmico e que o aumento da temperatura da água de processo é de 40 °C; e
(c) A eficiência de utilização da planta.
Passo 1
Beleza! Então, a primeira coisa que vamos fazer é desenhar o diagrama T-s do sistema descrito no enunciado, com o auxílio da tabela fornecida no enunciado e do diagrama já com os pontos de interesse, então, teremos:
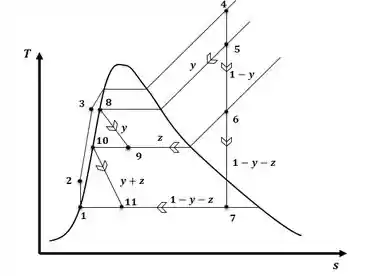
Passo 2
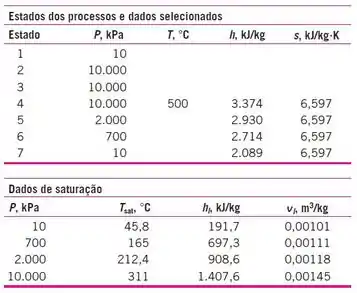
O que devemos fazer agora é pegar as propriedades do fluido faltantes nos pontos de interesse com os dados fornecidos no enunciado, então, com a ajuda das tabelas termodinâmicas do apêndice A, temos:
Com esse valor, podemos encontrar o trabalho específico exigido pela bomba 1 e depois encontrar a entalpia no ponto 2, então teremos:
E, aplicando o equilíbrio de energia específica para a bomba 1, temos:
Agora, continuando com as propriedades, temos:
E, como sabemos que temos líquido sub resfriado no ponto 3 e a mesma temperatura de 8, então teremos também a mesma entalpia, de forma que:
E, sabemos também que os purgadores de vapor podem ser considerados instrumentos isentálpicos, então temos:
Da mesma forma, temos no ponto 10:
E, como temos um purgador de vapor entre os estados 10 e 11, teremos:
Com esses valores, podemos aplicar um equilíbrio de energia específica para o aquecedor de água de alimentação fechado, o que nos dá:
Como temos regime permanente, então e a equação acima se torna:
Então, com isso, substituindo os valores em função das entalpias e da fração mássica, temos:
Então, isolando e substituindo os valores conhecidos, temos:
Substituindo os valores conhecidos, temos:
Passo 3
Então, agora podemos resolver a letra b). Vamos escrever o calor gerado na unidade de processamento térmico em função da variação de entalpia nesse dispositivo, então, temos:
E, como não há perda de calor nesse dispositivo, então, esse calor do processo será igual a energia fornecida pela água, que é dada por:
Então, igualando as duas expressões, temos:
Então, substituindo os valores conhecidos, temos:
Passo 4
Agora, para encontrar a eficiência de utilização da planta, precisamos da potência líquida produzida, da taxa de calor do processo e da taxa de calor que entra no sistema. A potência líquida produzida na usina é a diferença entre a potência produzida na turbina e a potência consumida pela bomba, dessa forma, temos:
Então, reescrevendo a equação com o auxílio do diagrama do passo 1 em função das entalpias e das frações mássicas, temos:
Substituindo os valores conhecidos, temos:
E, agora, para encontrar o valor na unidade de processamento térmico, vamos aplicar o equilíbrio de energia nesse ponto, que resultará na diferença de entalpias conforme visto na equação 10-27 nessa seção. Então, no nosso caso, temos:
Substituindo os valores conhecidos, temos:
E agora, para o calor que entra na caldeira, vamos nos basear na equação 10-25 apresentada nessa seção, e para o nosso caso, teremos:
Então, finalmente podemos calcular a eficiência de utilização da usina, dada por: