Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 3.Problemas - Ex. 17

  1. Deduza a expressão geral para o trabalho por quilomol de um gás de van der Waals em expansão reversível e a uma temperatura constante T, a partir de um volume especifico V 1 para um volume especifico V 2 .
  2. Usando as constantes da tabela 2.1, encontre o trabalho feito quando 2 quilomoles de vapor se expandem de um volume de 30 m 3 para um volume de 60 m 3 a uma temperatura de 100°C.
  3. Encontre o trabalho de um gás ideal na mesma expansão.

Passo 1

Faaaaaala, galera... Tranquileba??

Para a)

Sabemos que a equação de estado para um gas Van Der Waals:

P = n R T V - n b - a n 2 V 2

Pede o trabalho por mol, logo:

W n = - ∫ P   d V

Substituindo, temos:

W n =   - ∫ V 1 V 2 n R T V - b - a V 2 d V

W n = - ∫ V 1 V 2 n R T V - b d V - ∫ V 1 V 2 a V 2 d V

Separando a primeira integral:

∫ V 1 V 2 n R T V - b d V

Façamos V - b = U de forma que d U = d V

n R T ∫ V 1 V 2 1 U d U = n R T ln ⁡ U V 1 V 2

Substituindo U de volta:

∴ ∫ V 1 V 2 R T V - b d V = R T ln ⁡ V 2 - b V 1 - b

Para a segunda integral:

∫ V 1 V 2 a V 2 d V

∫ V 1 V 2 a V 2 d V = a V - 2 + 1 - 2 + 1 ​ V 1 V 2 = a   - 1 V 2 + 1 V 1

Assim:

W n = - ∫ V 1 V 2 R T V - b d V - ∫ V 1 V 2 a V 2 d V = R T ln ⁡ V 2 - b V 1 - b + a   1 V 2 - 1 V 1

Bora pro próximo passo?!

Passo 2

Obrigado por vir.

Para b)

Olhando para a tabela:

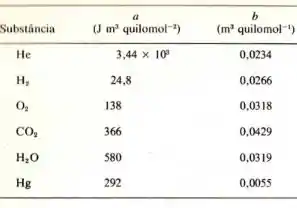
Sendo o Vapor, então é para H 2 O

Colocando valores:

W 2000 = 8.314 373,15 ln ⁡ 60 - 0.0319 30 - 0.0319 + 580   1 60 - 1 30 → W = 4 . 26 × 10 6 J

Passo 3

Para c)

Para o gás ideal:

W = - ∫ V 1 V 2 P   d V =   ∫ V 1 V 2 n R T V   d V = - n R T ln ⁡ V 2 V 1

W = 2000 8.314 373,15 ln ⁡ 60 30 = 4.3 × 10 6   J

Resposta

Para a)

W n = R T ln ⁡ V 2 - b V 1 - b + a   1 V 2 - 1 V 1

Para b)

4.26 × 10 6 J

Para c)

4.3 × 10 6   J

Exercícios de Livros Relacionados

Reconsidere o Prob. 8–57. Usando o EES (ou outro programa), estude o efeito de uma variação de 100 m/s até 300 m/s na velocidade de saída do bocal sobre a temperatura de saída e sobre a exergia destru
2.7 Um elevador transporta quatro pessoa, massa total igual a 300 kg, numa ascensão de 25 m. Explique qual é a transferância e a acumulação de energia no processo.
2.27 A aceleração “normal” da gravidade (ao nível do mar e a 45° de latitude) é 9,80665 m / s 2 . Qual é a força necessária para mantar imobilisada uma massa de 2kg neste campo gravitacional? Calcule
2.36 Um balde contendo concreto, com massa total igual a 200 kg, é movimentado por um guindaste. Sabendo que a aceleração do balde em relação ao chão, é 2 m / s 2 , determine a força realizada pelo gu
2.30 A variação da aceleração da gravidade, g, com a altura, z, pode ser aproximada por g = 9,807 - 3,32 × 10 - 6 z , onde a altura está em metros e a aceleração em m / s 2 . Determine a variação perc