Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 15.Problemas - Ex. 11
Em um determinado local, duas ondas sonoras harmônicas têm a mesma amplitude de deslocamento, mas a frequência do som A é o dobro da frequência do som B. Como suas densidades de energia médias se comparam?
(a) A densidade de energia média de A é duas vezes a densidade de energia média de B.
(b) A densidade de energia média de A é quatro vezes a densidade de energia média de B.
(c) A densidade de energia média de A é 16 vezes a densidade de energia média de B.
(d) Você não pode comparar as densidades de energia médias dos dados fornecidos.
Passo 1
Fala galera, beleza? Espero que sim! Então, nessa questão temos que: A densidade de energia média de uma onda sonora é dada por:
onde é a densidade média do meio, é a amplitude de deslocamento das moléculas que constituem o meio e ω é a frequência angular das ondas sonoras.
Passo 2
Expresse a densidade de energia média de som A:
A densidade média de energia do som B é dado por:
Dividindo a primeira dessas equações pelo segundo produz:
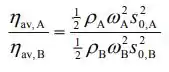
Porque as ondas sonoras são idênticas, exceto por suas frequências:
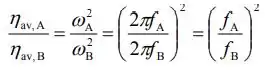
Como :
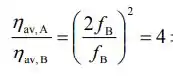
Logo, está correta.