Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 9.Problemas - Ex. 95
Determine a eficiência isoentrópica do compressor de R-134a analisado no Exemplo 6.10. Admita que o compressor ideal é adiabático.
Passo 1
Tudo bem galera? Vamos analisar essa questão.
Para o processo temos o seguinte diagrama T-s:
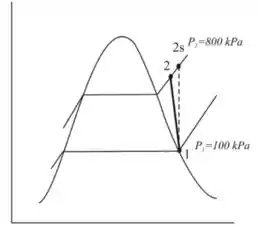
A entrada de energia isoentrópica do compressor é dada por:
Para a condição de entrada, a partir das tabelas de propriedades termodinâmicas, temos que:
Passo 2
Como a compressão é isoentrópica, temos que:
De acordo com a tabela de propriedades termodinâmicas, temos que:
A temperatura pode ser encontrada por interpolação:
E:
Passo 3
Aplicando a equação do Passo 1, temos que:
A eficiência de compressor é dada por:
A eficiência isoentrópica do compressor é de:
Resposta
Exercícios de Livros Relacionados
Reconsidere as condições operacionais descritas no Prob.7.25. Determine se é possível operar uma bomba de calor com os dados fornecidos. As operações satisfazem a primeira e a segunda lei da termodinâ
Considere um ciclo térmico motor que opera nas seguintes condições:a. Q ˙ H = 6k W Q ˙ L = 4 k W W ˙ = 2 k W b. Q ˙ H = 6k W Q ˙ L = 0 k W W ˙ = 6 k W c. Q ˙ H = 6k W Q ˙ L = 2 k W W ˙ = 5 k W d. Q ˙
Discuta os fatores que tornariam irreversível o ciclo de potência descrito no Prob. 6.99.
A água contida numa lagoa com pequena profundidade aquece durante o dia e é resfriada durante a noite. As transferências de calor por radiação, convecção e condução provocam esta flutuação cíclica de
Discuta os fatores que tornariam irreversível o ciclo da bomba de calor descrito no Prob.6.106.