Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 15
Determine o trabalho de fronteira realizado durante um processo de expansão, considerando que os valores da pressão e do volume em vários estados são medidos como 300 kPa, 1 L; 290 kPa, 1,1 L; 270 kPa, 1,2 L; 250 kPa, 1,4 L; 220 kPa, 1,7 L e 200 kPa, 2 L.
Passo 1
Para determinar o trabalho total realizado nesse processo, devemos plotar todos os pontos de pressão e volume num diagrama P-V.
Devemos relembrar que o trabalho pode ser definido como:
Devemos lembrar também que o significado de uma integral é a área embaixo de uma curva.
Logo, para calcular o valor do trabalho de fronteira, devemos plotar um gráfico e calcular a área da figura que se forma.
Passo 2
Devemos, primeiro, organizar os dados de pressão e volume em uma tabela. Além disso, para que possamos calcular o trabalho em devemos converter os valores de volume de L para m³, lembrando que 1 L vale 0,001 m³:
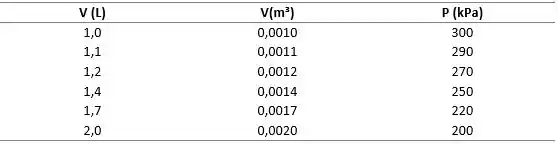
Com esses dados, podemos plotar o gráfico no Excel (ou em qualquer software de sua preferência):
Resposta
É possível notar que o gráfico tem uma tendência linear, e a figura geométrica abaixo da curva é um trapézio. Devemos lembrar, então, a fórmula da área de um trapézio:
Ao comparar com o nosso gráfico, podemos notar que a base maior do trapézio se trata da pressão de 300 , enquanto a base menor trata-se da pressão de 200 e a altura é a variação de volume entre os estados 1 e 2. Assim:
O sinal positivo indica que trabalho foi realizado pelo sistema.