Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 2.Problemas - Ex. 70
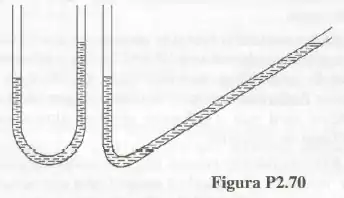
A diferença de altura das colunas de água num manômetro em U é igual a . Qual é a pressão relativa? Se o ramo direito do manômetro for inclinado do modo indicado na (o ângulo entre o ramo direito e a horizontal é ) e supondo a mesma diferença de pressão qual será o novo comprimento da coluna?
Passo 1
Oi pessoal, tudo certo? Vamos analisar essa questão!
Sabemos que a diferença de pressão relacionada à diferença de alturas de um fluido manométrico é dada por:
Portanto, é só calcular essa diferença de pressão para a condição de trabalho com um fluido de e :
Ou:
Passo 2
Se a configuração do tubo em U mudasse como apresentado na figura do enunciado, poderíamos relacionar a diferença de altura conhecida com a nova diferença no comprimento de fluido do tubo inclinado:
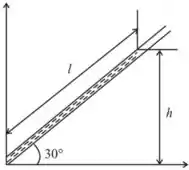
Fazendo as relações trigonométricas, temos que:
Logo: