Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 2.Problemas - Ex. 61
Uma das extremidades de um manómetro em U está conectada a uma tubulação e a outra está exposta ao ambiente (). A diferença entre as alturas das colunas de fluido manométrico é e a altura da coluna adjacente de tubulação é maior do que a outra. Sabendo que a massa especifica do fluido manométrico é . determine a pressão absoluta no interior da tubulação.
Passo 1
Oi pessoal, tudo certo? Vamos analisar essa questão!
Para responder esta questão, é importante visualizar a situação de maneira correta. Observe na Figura 2.11 do seu livro que a pressão no manômetro pode ser comum ou de vácuo e isso é importante nos nossos cálculos.
Observe que em uma a pressão absoluta é maior que a pressão atmosférica e na outra situação é menor. Vamos fazer um esboço da situação do enunciado.
Antes de esboçar, temos que ler atentamente o enunciado. Nele temos duas informações de extrema importância... Nos é dito que a diferença entre as alturas das colunas de fluido é de e que a altura da coluna adjacente de tubulação é maior que a outra.
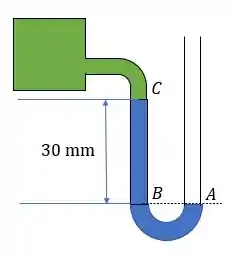
Ou seja... A altura do fluido manométrico é maior na parte que é ligada à tubulação e não na parte que está exposta ao ambiente. Desta forma, temos a seguinte situação:
Passo 2
Certo... A parte branca do esboço é a parte do tubo que está exposta ao ambiente e que sofre ação da pressão atmosférica.
A parte azul é a que contém o líquido manométrico e a parte verde é aquela que contém o fluido presente na tubulação. O exercício quer saber a pressão absoluta exatamente ali... na tubulação, ou pressão no ponto C.
Bom... nós já aprendemos a fazer o balanço de pressões em tubos U, é só pegar um ponto em comum e igualar. Ou seja, a pressão no ponto B deve ser a mesma que no ponto A, portanto:
Ou:
Portanto, a pressão absoluta será:
Passo 3
Vamos aos cálculos... Substituindo os dados da questão temos que:
Ou: