Dois quilogramas de ar em um conjunto cilindro-pistão executa um ciclo de potência de Carnot com temperaturas máxima e mínima de 750 K e 300 K, respectivamente. A transferência de calor para o ar, durante a expansão isotérmica, é de 60 kJ. Ao final da expansão isotérmica, o volume é de 0,4 m3. Admitindo o modelo de gás ideal para o ar, determine
(a) a eficiência térmica.
(b) a pressão e o volume no início da expansão isotérmica em kPa e m3, respectivamente.
(c) o trabalho e a transferência de calor para cada um dos quatro processos, em kJ.
(d) Esboce o ciclo em coordenadas p–V.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
a) Calculando a eficiência térmica do ciclo
Passo 3
b) Calculando a temperatura no final da expansão isotérmica no estado 4. Considerando a equação de gás ideal
Passo 4
Calculando o volume no começo da expansão isotérmica no estado 1. Aplicando a equação para o processo adiabático
Calculando a pressão no começo da expansão isotérmica. Considerando a equação do gás ideal
Passo 5
c) Calculando o trabalho e transferência de calor para cada um dos quatro processos
Processo 3-2: Expansão Isotérmica
Já que o processo isotérmico . Escrevemos a primeira lei da termodinâmica
Já que temos
Passo 6
Processo 4-1: Expansão Adiabática
Calculando a transferência de calor. Já que é um processo adiabático
Calculando o trabalho feito para o processo 4-1
Passo 7
Processo 1-2: Compressão Isotérmica
Escrevendo a relação para a transferência de calor e temperatura para um ciclo reversível operando entre dois reservatórios térmicos
Já que é um processo isotérmico,
Passo 8
Processo 2-3: Compressão Adiabática
Já que é um processo adiabático, a transferência de calor é
Calculando o trabalho feito, considerando a equação da primeira lei da termodinâmica para o processo cíclico
Passo 9
d) Desenhando o ciclo
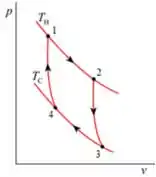
Resposta
a)
b)
c)