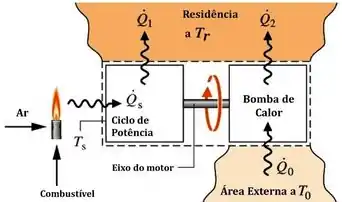
A Fig. P5.92 mostra um sistema que consiste em um ciclo de potência acionando uma bomba de calor. Em regime permanente, o ciclo de potência recebe por transferência de calor a da fonte de alta temperatura e fornece para uma residência a . A bomba de calor recebe do exterior a e fornece para a residência.
Usando a Eq. 5.13, obtenha uma expressão para o valor teórico máximo do parâmetro de desempenho em termos das razões de temperatura e .
Passo 1
Se você não tiver o livro original, não precisa se preocupar com a imagem pois a gente da equipe do Responde Aí facilita sua vida sempre e limpou a figura pra você gabaritar nessa questão e na sua prova. Então, vem com a gente.

Supondo que o sistema mostrado na figura está em estado estacionário, o valor teórico máximo para é obtido na AUSÊNCIA DE IRREVERSIBILIDADES INTERNAS.
Isso significa que o equilíbrio da taxa de energia para o sistema reduz para a seguinte condição:
Melhorando, em termos das nossas incógnitas temos:
Com essa suposição, podemos utilizar a Eq 5.7 para escrever as equações de cada máquina, onde:
Para o CICLO DE POTÊNCIA:
Para a BOMBA DE CALOR:
Passo 2
A razão pode ser exposta conforme a relação seguir, pelas equações escritas acima, onde:
Inserindo os valores dessa relação nas equações do Passo 1 e resolvendo para isolar , temos:
Isolando :
Passo 3
A partir daqui, podemos escrever todo o problema em função APENAS de , e exatamente como a questão pede onde:
Colocando os valores em já função das razões de temperatura e , ficamos com: