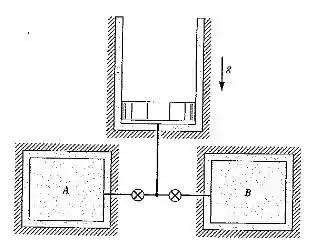
Dois tanques, contendo vapor, estão conectados a um conjunto cilindro-pistão, conforme mostrado na Fig. P8.52. Inicialmente, o pistão está no fundo do cilindro e a massa do pistão é tal que uma pressão de embaixo dele será capaz de levantá-lo. O vapor A tem uma massa de e e e, em B, tem uma massa de a e . As duas válvulas são abertas e a água chega a um estado uniforme. Determine a temperatura final e a geração total de entropia admitindo que não exista transferência de calor.

Cálculo do tanque A, com volume específico, energia interna e entropia correspondente a

Da tabela de água superaquecida B.1.3, com os valores correspondentes a e , podemos encontrar o volume específico do tanque B, entropia e energia interna:

Calculando os volumes dos tanques A e B:

O volume final é a soma dos dois iniciais:

E a massa final é igual a

A partir da equação de energia, podemos calcular a entalpia específica do estágio 2:

Fazendo a substituição dos termos

Da tabela de água superaquecida B.1.3, com os valores correspondentes a e , nós podemos encontrar a entropia específica e a temperatura:

Calculando a entropia específica final e a temperatura correspondente a e usando o método de interpolação linear:

E para a temperatura

Com isso, a variação de entropia é dada por

Fazendo a substituição dos termos