A energia de Gibbs em excesso para sistemas binários constituídos por líquidos não muito dissimilares na natureza química tem uma representação com razoável aproximação pela equação:
onde É uma função de temperatura somente. Para tais sistemas, é observado frequentemente que a razão das pressões de vapor das espécies puras é aproximadamente constante em uma faixa considerável de temperaturas. Considere essa razão igual a , e determine a faixa de valores de , expressa em função de , na qual não pode existir azeótropo. Admita que a fase vapor é um gás ideal.
Passo 1
ENCONTRADO: Determine a análise em termos de frações de massa, a pressão parcial de cada componente, o volume ocupado por 50 kg de mistura.
ESQUEMA DADOS FORNECIDOS:

PREMISSAS: (1) A mistura geral atua como um gás ideal. (2) Cada componente da mistura se comporta como se fosse um gás ideal ocupando todo o volume na temperatura da mistura. (3) Os cálculos são baseados em 1 kmol de mistura na parte (a).
ANÁLISE: (a) Considerando um típico 1 kmol de mistura
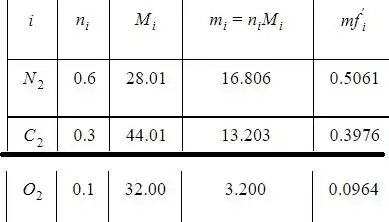
Passo 2
Passo 3
Usando a avaliação de estado de gás ideal
O peso molecular aparente da mistura é obtido nos cálculos da parte (a). Equivalentemente, Eq 9,12.9 pode ser usado