Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 118

Ar entra a 310   K   e   100   k P a no compressor de um motor de turbina a gás com regeneração, onde é comprimido até 900   k P a   e   650   K . O regenerador tem uma efetividade de 80 % , e o ar entra na turbina a 1.400   K . Para uma eficiência da turbina de 90 % , determine (a) a quantidade de calor transferida no regenerador e (b) a eficiência térmica. Considere calores específicos variáveis para o ar.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

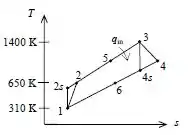
Bom... Para esboçar o nosso ciclo em um diagrama T - s , temos que saber primeiramente se os processos de compressão e expansão serão totalmente isentrópicos ou não.

No caso a turbina não é totalmente isentrópica, então teremos o estado ideal 4 s e o estado real 4 .

O exercício nos disse que a pressão na entrada do compressor é de 100   k P a e na entrada do regenerador é de 900   k P a . Para o ciclo com regeneração, teremos que:

P 1 = P 4 = P 6 = 100   k P a

P 3 = P 2 = P 5 = 900   k P a

Ou seja:

r p = 900 100

r p = 9

Como o ar entra no compressor a 310   K , no regenerador a 650   K e na turbina a 1 4 00   K , temos que:

T 1 = 310   K

T 2 = 650   K

T 3 = 1 4 00   K

O ciclo Brayton real com regeneração é dado por:

Passo 2

Agora vamos analisar os processos:

Considerando calores específicos variáveis com a temperatura teremos que encontrar na tabela suas respectivas propriedades de entalpia e pressão relativa para calcular as propriedades dos outros estados desconhecidos.

Temos que, para T 1 = 310   K :

h 1 = 310,24   k J / k g

Para T 2 = 650   K , temos que:

h 2 = 659,84   k J / k g

E, para:

T 3 = 1 4 00   K h 3 = 1 515,42 k J k g P r 3 = 450,5

Portanto, sabendo que:

P r 4 P r 3 = 1 r p

Temos que:

P r 4 = 450,5 9

P r 4 = 50,06

Passo 3

A partir do valor encontrado no passo anterior, podemos interpolar com o auxilio da tabela, sua respectiva entalpia correspondente:

h 4 s = 821,95 + 843,98 - 821,95 50,05 - 47,75 52,59 - 47,75

h 4 s = 832,418   k J / k g

Esta é a entalpia ideal, porém, a turbina não é totalmente isentrópica, portanto a sua entalpia real será:

h 4 = h 3 - η t h 3 - h 4 s

h 4 = 1515,42 - 0,9 1515,42 - 832,418

h 4 = 900,718   k J / k g

Como a efetividade do regenerador é de 8 0 % , temos que:

q r e g e n = ϵ h 4 - h 2

q r e g e n = 0,8 900,718   - 659,84

q r e g e n = 192,7   k J / k g

Passo 4

A eficiência térmica é dada por:

η = w l i q q e n t

Como:

w l i q = w t u r b - w c o m p

w l i q = h 3 - h 4 - h 2 - h 1

w l i q = 1515,42 - 900,718 - 659,84 - 310,24 = 265,08   k J / k g

E:

q e n t = h 3 - h 2 - q r e g e n

q e n t = 1515,42 - 659,84 - 192,7

q e n t = 662,88   k J / k g

Temos que:

η = 265,08 662,88

η = 0,4

Ou:

η = 40 %

Resposta

a )   q r e g e n = 192,7   k J / k g

b ) η = 40 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um ciclo Brayton simples ideal é modificado para incorporar compressão de múltiplos estágios com resfriamento intermediário, expansão de múltiplos estágios com reaquecimento e regeneração sem variar o
Em um ciclo de turbina a gás ideal com resfriamento intermediário, reaquecimento e regeneração, à medida que a quantidade de estágios de compressão e expansão aumenta, a eficiência térmica do ciclo se
Em 1903 , Aegidius Elling, da Noruega, projetou e construiu uma turbina a gás de 11h p , que usava injeção de vapor de água entre a câmara de combustão e a turbina para resfriar os gases de combustão
Quais modificações são necessárias para que o ciclo de turbina a gás simples ideal se aproxime do ciclo Ericsson?
Defina a eficiência de um regenerador usado em ciclos de turbina a gás.