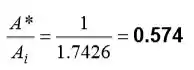Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 17.Problemas - Ex. 62
Ar entra em um bocal a , e a uma velocidade de . Aproximando as condições para um fluxo isentrópico, determine a pressão e a temperatura do ar em um local onde a velocidade do ar iguala-se à velocidade do som. Qual é a razão entre a área nesse local para a área de entrada?
Passo 1
Vamos lá! O ar entra num bico à temperatura, pressão e velocidade especificadas. A pressão de saída, a temperatura de saída e a relação entre a área de saída e a entrada devem ser determinadas para um número de Mach de Ma = 1 na saída.
Passo 2
As propriedades do fluido no local onde são as propriedades críticas, denotadas por superescrito *. A temperatura e pressão de estagnação neste caso são idênticas à temperatura e pressão de entrada, uma vez que a velocidade de entrada é insignificante. Elas permanecem constantes em todo o bico, uma vez que o fluxo é isentrópico.
Passo 3
As propriedades do fluido no local onde são as propriedades críticas, denotadas por superescrito *. Primeiro determinamos a temperatura e pressão de estagnação, que permanecem constantes ao longo do bico, uma vez que o fluxo é isentrópico.
Da Tabela A-32 (ou de Eqs. 17-18 e 17-19) em , lemos Assim,
E,
Também temos que,
E,
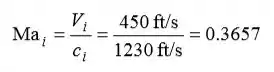
Da Tabela A-32 neste número de Mach lemos . Assim, a razão entre a área da garganta e a área de entrada do bico é
