Ar entra no compressor de um ciclo de refrigeração Brayton a 100 kPa e 260 K e é comprimido adiabaticamente até 300 kPa. O ar entra na turbina a 300 kPa e 300 K e expande-se adiabaticamente até 100 kPa. Para esse ciclo
(a) determine o trabalho líquido por unidade de massa de ar, em kJ/kg, e o coeficiente de desempenho se as eficiências isentrópicas do compressor e da turbina forem ambas de 100%.
(b) esboce graficamente o trabalho líquido por unidade de massa de ar, em kJ/kg, e o coeficiente de desempenho para iguais eficiências isentrópicas do compressor e da turbina para um intervalo de 80% a 100%.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
O diagrama que representa o ciclo de Brayton
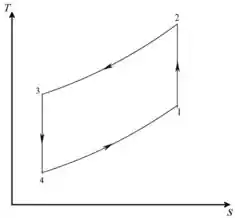
Passo 3
Pegamos os valores de e da tabela de propriedade do ar como gás ideal, usando a temperatura na entrada do compressor
Calculamos o valor de usando
Passo 4
Pegamos os valores de no ponto 2 da tabela de propriedade do ar como gás ideal, interpolando entre e
Pegamos os valores de e da tabela de propriedade do ar como gás ideal, usando a temperatura na entrada do compressor
Calculamos o valor de usando
Passo 5
Pegamos os valores de no ponto 4 da tabela de propriedade do ar como gás ideal, interpolando entre e
O trabalho no compressor é dado por
O trabalho da turbina é dado por
O trabalho líquido total de entrada do ciclo por unidade de massa é dado por
Passo 6
Determinamos a capacidade de refrigeração usando
O coeficiente de performance do ciclo é dado por
Passo 7
Considerando o ciclo de refrigeração de Brayton atual
Podemos plotar valores para o trabalho líquido X eficiência e X eficiência
Consideramos a seguinte expressão para o trabalho do compressor e da turbina em termos da eficiência isentrópica
Então, temos que o trabalho líquido do ciclo é
Considerando o processo atual de expansão 3-4, e o processo isentrópico 3-4s
Calculando a capacidade de refrigeração do ciclo atual
Determinando o coeficiente de performance do ciclo
Passo 8
Variando de 80% a 100% podemos plotar os resultados
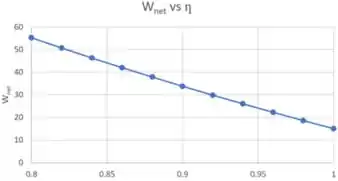
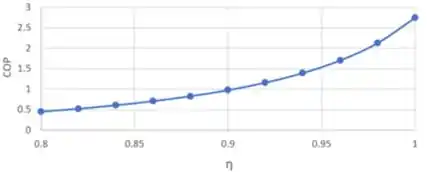
Combinando os dois:
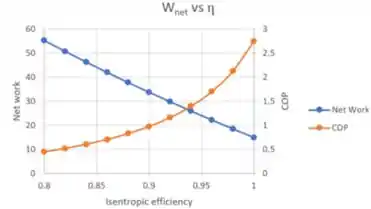
Resposta
a)