Ar entra no compressor de um ciclo de refrigeração Brayton a 100 kPa, 270 K. A razão de pressão do compressor é 3 e a temperatura na entrada da turbina é 315 K. O compressor e a turbina apresentam eficiências isentrópicas de 82% e 85%, respectivamente. Determine o
(a) trabalho líquido de acionamento, por unidade de massa de ar, em kJ/kg.
(b) balancete exergético da potência de acionamento do compressor, em kJ por kg de ar. Discuta o resultado.
Admita T0 = 315 K.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
Desenhando o diagrama do ciclo de Brayton
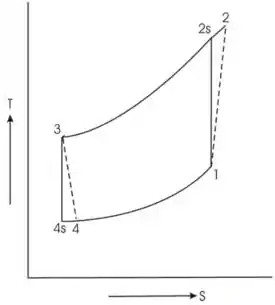
Passo 3
Pegando as propriedades do ar na entrada do compressor. A temperatura de e pressão de
Calculando a razão de pressão isentrópica na saída do compressor
Com essa razão de pressão, obtemos a entalpia isentrópica do ar na saída do compressor usando interpolação da Tabela A-22 “Propriedades do Ar como Gás Ideal”
Passo 4
Escrevendo a expressão para a eficiência do compressor
Da Tabela A-22 “Propriedades do Ar como Gás Ideal”, obtendo a entropia do ar na saída do compressor usando interpolação
Passo 5
Obtendo as propriedades do ar na entrada da turbina a temperatura de
Calculando a razão de pressão na saída da turbina
Da Tabela A-22 “Propriedades do ar como Gás Ideal” obtemos a entalpia isentrópica do ar na saída da turbina a usando interpolação
Escrevendo a expressão para a eficiência isentrópica da turbina
Da Tabela A-22 “Propriedades do Ar como Gás Ideal” com
Passo 6
a) calculando o trabalho de entrada por unidade de massa do fluxo de ar
Passo 7
b) calculando a taxa de destruição de exergia no compressor
Passo 8
Calculando a exergia perdida através do trocador de calor
Passo 9
Calculando a taxa de destruição de exergia na turbina
Passo 10
A disposição da exergia de entrada total
Trocador de calor
Compressor
Turbina
A contribuição total de exergia é
Resposta
a)