Reconsidere o Problema 10.50, mas inclua na análise o fato de o compressor e a turbina terem eficiências isentrópicas, respectivamente, iguais a 85% e 88%. Responda às mesmas perguntas do Problema 10.50.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?! Recomendo que você dê uma voltada na questão 50 pra relembrar o que a gente fez lá, beleza?
O que vai mudar da 50 pra essa é que a gente vai ter dois processos intermediários, devido a eficiência, 2s e 4s.
Passo 2
O diagrama é mostrado abaixo
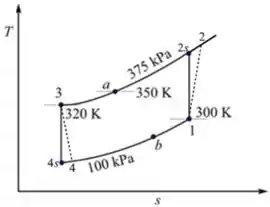
Passo 3
Obtendo as propriedades do ar no estado 1
Com temperatura de entrada de , pegamos as propriedades da Tabela A-22 “Propriedades do Ar Como Gás Ideal”
Passo 4
Calculando a pressão relativa no estado 2
Aplicando a relação de processo isentrópico
Calculando a entalpia no estado 2s
Com a pressão relativa obtida , pegamos as propriedades da Tabela A-22 “Propriedades do Ar Como Gás Ideal”, interpolando
Calculamos a entalpia no estado 2 usando
Passo 5
Obtendo as propriedades do ar no estado
Com temperatura de entrada de , pegamos as propriedades da Tabela A-22 “Propriedades do Ar Como Gás Ideal”
Passo 6
Obtendo as propriedades do ar no estado 3
Com temperatura de entrada de , pegamos as propriedades da Tabela A-22 “Propriedades do Ar Como Gás Ideal”
Passo 7
Calculando a pressão relativa no estado 4
Aplicando a relação de processo isentrópico
Calculando a entalpia no estado 4s
Com a pressão relativa obtida , pegamos as propriedades da Tabela A-22 “Propriedades do Ar Como Gás Ideal”, interpolando
Calculamos a entalpia no estado 4 usando
Passo 8
a) Calculando a menor temperatura em
Com a pressão relativa obtida , pegamos as propriedades da Tabela A-22 “Propriedades do Ar Como Gás Ideal”, interpolando
Passo 9
Calculando a entalpia no estado
Aplicando o balanço de energia
Passo 10
Calculando a entrada do calor no compressor por unidade de massa do fluxo de ar
Calculando a entrada do calor na turbina por unidade de massa do fluxo de ar
Passo 11
b) Calculando o trabalho líquido de entrada por unidade de massa
Passo 12
c) Calculando a capacidade de regeneração por unidade de massa
Passo 13
d) calculando o coeficiente de performance do ciclo
Resposta
a)
b)
c)
d)