Ar entra no compressor de uma turbina a gás de uma usina termoelétrica a 70ºF (21.1 ºC), 1 atm, é comprimido adiabaticamente para 40 lbf/in² (275.8 kPa), e em seguida entra na câmara de combustão, onde queima completamente com gás propano (que entra a 77ºF (25 ºC), 40lbf/in² (275.8 KPa) e uma vazão molar de 1.7 lbmol/h. Os produtos de combustão a 1340 ºF (727 ºC) e 40lbf/in² entram na turbina e se expandem adiabaticamente até a pressão 1 atm. A eficiência isentrópica do compressor é de 83.3% e a eficiência isentrópica da turbina é de 90%. Determine, em regime permanente,
o percentual de ar teórico necessário.
a potência liquida desenvolvida, em hp.
Passo 1
Espero que esteja bem e pronto para aprender a resolver mais uma questão de Termodinâmica.
Vamos recapitular o que sabemos até então sobre a questão.
Os dados da questão são fornecidos para uma turbina a gás simples operando em regime permanente. O gás propano queima completamente na câmara de combustão.
O rascunho abaixo nos irá ajudar a entender o processo que está acontecendo:
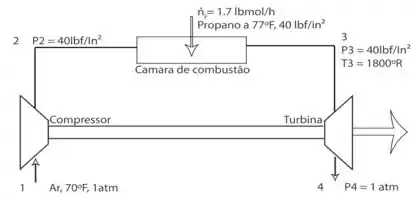
Antes de começar a resolver a questão, precisamos adotar algumas considerações:
(I) Os volumes de controle, incluindo vários componentes, conforme necessário, estão em estado estacionário;
(II) O compressor, a turbina e a câmara de combustão são adiabáticas;
(III) O combustível, ar e produtos de combustão são modelados como gás ideal;
(IV) Os efeitos da energia cinética e potencial são desprezíveis;
(V) 3,76 moles de N₂ inerte acompanham cada mol de O₂ no ar de combustão;
(VI) Combustão considerada completa.
Passo 2
Depois de muitas considerações iremos agora para a felicidade de todos e bem geral da nação, começar a resolver a questão. UFAAA!!!
Vamos montar primeiro a equação balanceada da situação da questão;
Um balanço de taxa de energia para a câmara de combustão mostra . Essa igualdade é super importante para podermos encontrar a nossa resposta, mas para isso precisamos antes encontrar o valor de .Para encontrarmos , iremos usar o dado que já nos foi dado, a eficiência do compressor: . Para encontrar , considere uma compressão isentrópica da mistura de ar assumida de = 21.1ºC, P1 = 1 atm para , 40lbf/in². Então temos que,
os valores foram obtidos na Tabela A-23E do livro, então vamos todos pegar a tabela antes de continuar a resolução.
Resolvendo por interação, o valor de temperatura que mais se aproxima a nossa situação é de 705 ºR, podemos então finalmente continuar para a próxima etapa da solução.
Passo 3
Todo o processo que realizamos anteriormente foi apenas para encontrar a , necessária para encontrarmos o que realmente importa nessa questão, o percentual de ar teórico necessário.
Temos que recorrer novamente às Tabelas do livro para encontrar os valores e substituir na nossa equação.
descobrimos então que mas também podemos escrever o que encontramos da seguinte forma,
Resolvendo interativamente temos que
Anteriormente encontramos que , por conta do balanço de taxa de energia, assim iremos utilizar essa relação em conjunto com para encontrar finalmente a resposta da nossa letra A.
3[
Com o auxílio da tabela A-25E e da tabela A-23E, temos que:
3[-169.300 + (18392-4028)] + 4[-104.040 + (15433-4258)] + 5(n-1)(13486-3725) + 18.8n(12956-3730) = -44.680 + 5n[5167-3725] + 18.8n[51443730]
Finalmente resolvendo essa equação, encontramos que nosso n é igual a 4.46, sendo assim temos que o percentual teórico de ar que tanto lutamos para encontrar é de 446% . UFAAAAA!
Passo 4
Espero que todos não tenha desistido da nossa amada Termodinâmica ainda, respirem que ainda temos a letra B da nossa questão.
A potência líquida desenvolvida é a diferença entre a potência de saída da turbina e a potência de entrada do compressor. Para encontrar a saída da turbina:
consequentemente, considere a seguir uma expansão isentrópica dos produtos de combustão de (726,5 ºC, 40 lbf/in²) para (, 1 atm), temos que e sendo assim,
Usando os dados da Tabela A-23,
O valor de que mais se aproxima é o de 1400 ºR. A potência que seria desenvolvida, por mol de combustível consumido, em uma expansão isentrópica é então
Para o compressor
Finalmente temos que a saída de potência líquida é:
Resposta
- 446% de ar teórico
- 102.4 hp