Fluxos de hidrogênio (H₂) e de oxigênio (O₂), cada qual a 1atm, entram em uma célula de combustível operando em regime permanente e vapor d’agua sai a 1atm. Se a célula de combustível opera isotermicamente a (a) 300K, (b) 400K, (c) 500K. Determine o trabalho teórico máximo que pode ser desenvolvido pela célula, em cada caso, em KJ por Kmol de hidrogênio que escoa, e comente. A transferência de calor com a vizinhança ocorre à temperatura da célula e os efeitos das energias cinética e potencial podem ser ignorados.
Passo 1
O que sabemos pelo enunciado é que os dados operacionais são fornecidos para uma célula de combustível em estado estacionário
O que queremos descobrir é o máximo trabalho teórico que se pode desenvolver
Iremos realizar as seguintes considerações no nosso sistema: (1) O volume de controle mostrado está em estado estacionário (2) Os efeitos da energia cinética e potencial são desprezíveis. (3) Estado de transferência de calor com o ambiente ocorre na temperatura da célula
Temos que ter em mente que está é uma questão que deve ser respondida por meio computacional, algo comum nesse livro que utiliza de soluções interativas. Dito isso, vamos para a equação química da nossa questão
Balanço de energia e entropia em estado estacionário, respectivamente
Eliminando a transferência de calor, e somando as equações temos,
De acordo com e , e notando que o máximo valor que queremos corresponder ao caso de nenhuma produção de entropia,
]
Passo 2
Para resolver iterativamente nossa questão iremos utilizar o seguinte código:
T = 300 //K
P = 1.01325 //bar
Wdot_max = - hfo_H2) + delh_H2 + .5*delh_02-delh_H2O-T*(so_H2+.5*so_O2 -so_H2O)
hfo_H20 = h_T(“H20”, 298.15)
delh_H2 = h_T(“H2”,T) -h_T(“H2”,298.15)
delh_O2 = h_T(“O2”,T) -h_T(“O2”,298.15)
delh_H2O = h_T(“H2O”,T) -h_T(“H2O”,298.15)
so_H2 = s_TP(“H2”,T,p)
so_O2 = s_TP(“O2”,T,p)
so_H2O = s_TP(“H2O”,T,p)
Passo 3
Os resultados que obtemos são
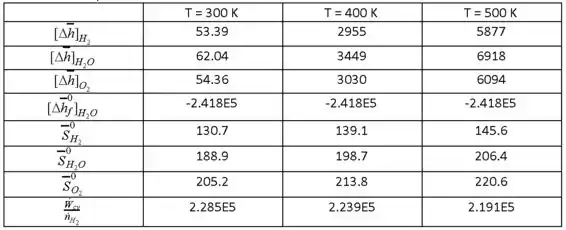
Resposta
A medida que T aumenta, diminui e as transferências de calor associadas aumentam. Em princípio, trabalho adicional poderia ser desenvolvido a partir da transferência de calor. O máximo obtido corresponde ao caso em que a transferência de calor é fornecida a uma potência reversível operando ciclicamente entre a célula à temperatura T e a vizinhança a : o trabalho máximo igual