Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 17.Problemas - Ex. 98
O ar que escoa a e ao número de Mach é imposto a uma cunha bidimensional de semiângulo . Determine os dois ângulos de choque oblíquo possíveis, e , que poderiam ser formados por essa cunha. Para cada caso, calcule a pressão, a temperatura e o número de Mach a jusante do choque oblíquo. Em seguida, compare e discuta.
Passo 1
Antes de tudo vamos para algumas considerações que serão adotadas para a resolução do nosso problema que são
- O fluxo é constante.
- A camada limite na cunha é muito fina.
- O ar é um gás ideal com constante.
Além disso, temos que a relação de calor específica do ar é . Desenhando a situação problema, vamos ter
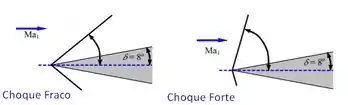
Nesse caso temos para o choque fraco e choque forte um associados, respectivamente.
Passo 2
Com base no que assumimos em vamos tomar um ângulo de deflexão igual ao meio ângulo da cunha, ou seja, , então, os dois valores do ângulo de choque oblíquo β são determinados a partir de
Agora temos uma equação que está implícita para e podemos resolver iterativamente ou utilizando algum software que resolva equações como por exemplo o Wolfram ou o EES. Assim, obteremos ,então, o número de Mach “normal” se torna
Além disso, os números normais a jusante se tornam
Passo 3
Pois bem, com as informações obtidas nos passos anteriores podemos calcular a pressão a jusante de cada caso é determinada como sendo
Por fim, o número de Mach a jusante é determinado como