Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 95

Escrevendo um balanço de energia para o trocador de calor de um ciclo binário a vapor, obtenha uma equação para a razão entre os fluxos de massa dos dois fluidos considerando suas entalpias.

Passo 1

Tá legal, a primeira coisa que vamos fazer é ilustrar o diagrama de uma usina que opera com um ciclo binário a vapor:

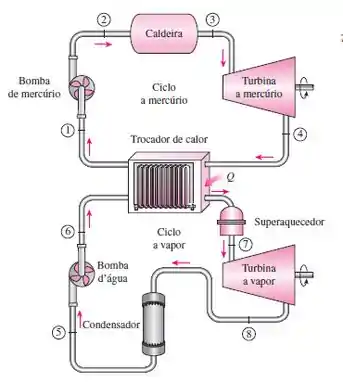
Note que nesse caso, o livro forneceu a imagem com um ciclo operando com vapor de água e mercúrio. No nosso caso, vamos chamar o ciclo superior de A e o ciclo inferior de B .

Passo 2

Então, tomando como base o diagrama do passo 1, vamos aplicar o equilíbrio de energia para o sistema, então, temos:

E ˙ e - E ˙ s = Δ E ˙

No nosso caso, temos regime permanente e também podemos desprezar as variações de energia cinética e potencial, então a equação se resume a:

E ˙ e = E ˙ s

Então, escrevendo isso em função das vazões mássicas dos ciclos A e B e das entalpias, temos:

m ˙ A h 4 + m ˙ B h 6 = m ˙ A h 1 + m ˙ B h 7 → m ˙ A h 4 - m ˙ A h 1 = m ˙ B h 7 - m ˙ B h 6

Colocando as vazões mássicas em evidência, temos:

m ˙ A h 4 - h 1 = m ˙ B h 7 - h 6 → m ˙ A m ˙ B = h 7 - h 8 h 4 - h 1

Resposta

m ˙ A m ˙ B = h 7 - h 8 h 4 - h 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é um circuito termoelétrico?
Um refrigerador reversível por absorção consiste em uma máquina térmica reversível e um refrigerador reversível. O sistema remove calor de um espaço resfriado a 15 °C a uma taxa de 70 kW. O refrigerad
Por que os materiais semicondutores são mais adequados do que os metais para os refrigeradores termoelétricos?
Um resfriador termoelétrico tem um COP de 0,15 e remove o calor de um espaço refrigerado a uma taxa de 180 W. Determine a entrada de potência necessária no resfriador termoelétrico, em W.
O calor é fornecido para um sistema de refrigeração por absorção de um poço geotérmico a 130 °C a uma taxa de 5 * 10 5 kJ/h. O ambiente está a 25 °C, e o espaço refrigerado é mantido a30 °C. Determine