Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 11.Problemas - Ex. 93
Um refrigerador reversível por absorção consiste em uma máquina térmica reversível e um refrigerador reversível. O sistema remove calor de um espaço resfriado a 15 °C a uma taxa de 70 kW. O refrigerador opera em um ambiente a 25 °C. Considerando que o calor é fornecido ao ciclo por vapor saturado e condensado a 150 °C, determine (a) a taxa com a qual o vapor se condensa e (b) a entrada de potência no refrigerador reversível. (c) Considerando que o COP de um resfriador (chiller) real por absorção nos mesmos limites de temperatura tem um COP de 0,8, determine a eficiência da segunda lei da termodinâmica para esse resfriador.
Passo 1
Oi pessoal, tudo bem?
Bem, o esboço do refrigerador pode ser:
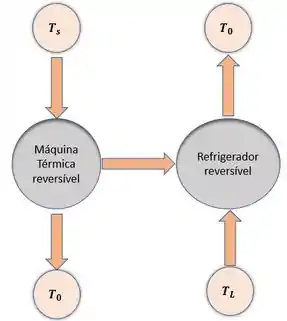
Primeiramente, como foram dadas as temperaturas ambiente e do calor fornecido, podemos encontrar a eficiência da máquina térmica:
O maior COP que o refrigerador pode ter é definido por:
Lembrando que e são as temperaturas termodinâmicas do espaço refrigerado, do
ambiente e da fonte de calor, respectivamente.
Então, transformando os valores das temperaturas para Kelvin e substituindo na equação, temos:
Passo 2
Letra a) Sabemos também, que o COP do refrigerador pode ser definido como:
Então:
Como a taxa de calor removido já foi informado e o COP encontrado, podemos descobrir a taxa máxima de calor que pode ser fornecido, assim:
Devemos lembrar também, que a vazão mássica pode ser informada como:
Em que é a entalpia de vaporização para a água a . Da tabela A-4 do livro texto, podemos encontrar . Então:
Passo 3
Letra b) A entrada de potência no refrigerador reversível pode ser definida como:
Então, substituindo os valores, temos:
Passo 4
Letra c) Para a análise da eficiência da segunda lei da termodinâmica para esse resfriador, podemos:
Resposta
Portanto:
Letra a)
Letra b)
Letra c)