Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 49

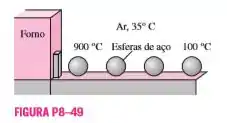
Esferas de aço-carbono ( ρ = 7833   k g / m 3   e   c p = 0,465   k J / k g ⋅ ° C )   de 8 mm de diâmetro são recozidas por aquecimento: para isso, são deixadas a 900 °C em um forno, e depois resfriadas lentamente até 100 °C em ar ambiente a 35 °C. Considerando que 1200 esferas tenham de ser recozidas por hora, determine (a) a taxa de transferência de calor das esferas para o ar e (b) a taxa de destruição da exergia decorrente da perda de calor das esferas para o ar.

Passo 1

Temos que o balanço de energia adotando uma esfera como sistema será dado por:

Q = Δ U ^ = m c p Δ T

A massa de cada esfera pode ser obtida através da seguinte expressão:

m = ρ V = ρ π D 3 6 = 7833   k g / m 3 × π 0,008   m 3 6 = 0,00210   k g

Assim, o calor perdido por cada esfera será de:

Q = 0,00210   k g × 0,465   k J / k g ⋅ ° C × 100 ° C - 900 ° C = - 0,781   k J

Para calcular a taxa de transferência de calor das esferas para o ambiente, teremos:

Q ˙ = t a x a   d e   e s f e r a s × Q = ( 1200   e s f e r a s / h ) × ( - 0,781   k J ) = - 936   k J / h = - 260 W

O sinal negativo está se referindo ao calor que sai da esfera.

Passo 2

A exergia destruída é dada pela seguinte expressão:

X d e s t r u í d a = T 0 S g e r

Ao fazer o balanço de entropia, chegaremos que a entropia gerada por cada esfera será dada por:

S g e r = Q T a m b i e n t e + Δ S s i s t e m a = Q T a m b i e n t e + m c p ln ⁡ T 2 T 1

S g e r = 0,718   k J 308   K + 0,00210   k g × 0,465 k J k g ⋅ K × ln ⁡ 373 1173 = 0,00142   k J / K

A taxa de geração de entropia pelas esferas é então:

S ˙ g e r = S g e r × t a x a   d e   e s f e r a s = 0,00142 k J K × 1200 e s f e r a s h = 1,704 k J h ⋅ K = 0,000473   k W / K

Assim, a taxa de exergia destruída será dada por:

X ˙ d e s t r u í d a = S ˙ g e r T 0 = ( 0,000473   k W / K ) × ( 308   K ) = 146   W

Resposta

Assim,

  1. 260 W;
  2. 146 W.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois poços geotérmicos têm conteúdos de energia considerados iguais. As exergias desses poços serão necessariamente iguais? Explique.
Considere um processo que não envolve irreversibilidades. O trabalho útil real desse processo será igual ao trabalho reversível?
A exergia de um sistema é diferente em ambientes diferentes?
Calcule a eficiência baseada na segunda lei da termodinâmica do trocador de calor contracorrente descrito no Prob. 9.61. Admita que a temperatura do ambiente é a 20 ° C .
Construa um processo reversível para mostrar explicitamente que a entropia aumenta durante a expansão livre de um gás ideal.