A Fig. P10.32 mostra um diagrama esquemático de um sistema de refrigeração por compressão de vapor com dois evaporadores que utiliza Refrigerante 134a como fluido de trabalho. Esse arranjo é utilizado para se obter refrigeração a duas temperaturas distintas e com um único compressor e um único condensador. O evaporador de baixa temperatura opera a -18ºC e com vapor saturado na saída, tendo uma capacidade frigorífica de 3 TR (10,5 kW). O evaporador de alta temperatura produz vapor saturado a 3,2 bar na sua saída e tem uma capacidade frigorífia de 2 TR (7 kW). A compressão, até uma pressão do condensador de 10 bar, é isentrópica. Não existem quedas de pressão significativas nos escoamentos ao longo do condensador e dos dois evaporadores. e o refrigerante deixa o condensador como líquido saturado a 10 bar. Calcule
(a) a vazão mássica do refrigerante em cada evaporador, em kg/min.
(b) a potência de acionamento do compressor, em kW.
(c) a taxa de transferência de calor do refrigerante que escoa pelo condensador, em kW.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
O diagrama é dado a seguir
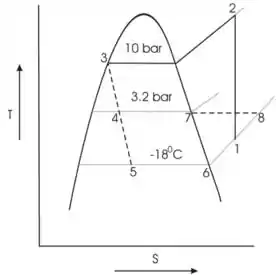
Passo 3
a) calculando a capacidade de refrigeração no evaporador 1
Das propriedades do Refrigerante 134a saturado (líquido-vapor) tabela de pressão a
Das propriedades do Refrigerante 134a saturado (líquido-vapor) tabela de temperatura a
Então, temos que
Passo 4
calculando a capacidade de refrigeração no evaporador 2
Das propriedades do Refrigerante 134a saturado (líquido-vapor) tabela de pressão a
Das propriedades do Refrigerante 134a saturado (líquido-vapor) tabela de pressão a
Então, temos que
Passo 5
b) no estado 1 temos uma mistura adiabática de 6 a 8. Aplicando a equação do balanço de energia
A temperatura de e entalpia das tabelas de R-134a superaquecido, usando interpolação dupla
Com pressão de e entropia das tabelas de R-134a superaquecido
Calculando a potência do compressor
Passo 6
c) a taxa de transferência do calor do refrigerante passando pelo condensador
Resposta
a)
b)
c)