A Fig. P10.34 fornece os dados de operação de um ciclo de refrigeração por compressão de vapor ideal em regime permanente, com Refrigerante 134a como fluido de trabalho. A bomba de calor fornece aquecimento a uma taxa de 15 kW para manter o interior de um edifício a 20°C quando a temperatura externa é de 5°C. Esboce o diagrama T–s do ciclo e determine

(a) as temperaturas nos estados principais do ciclo, ambas em °C.

(b) a potência de acionamento do compressor, em kW.

(c) o coeficiente de desempenho.

(d) o coeficiente de desempenho de um ciclo de bomba de calor de Carnot que opera entre reservatórios nas temperaturas interna e externa do edifício, respectivamente.

Compare os coeficientes de desempenho determinados em (c) e (d), e comente.

O diagrama do ciclo é mostrado abaixo

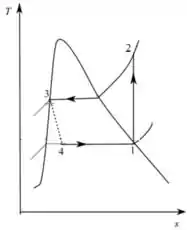
• Processo 1-2: compressão isentrópica no compressor
• Processo 2-3: rejeição de calor no condensador
• Processo 3-4: expansão de estrangulamento
• Processo 4-1: adição de calor no evaporador

a) Achando a temperatura do refrigerante no estado 1

Achando o valor da temperatura no estado 1 a pressão de , da Tabela A-11 “Propriedades de Refrigerante 134a Saturado: Tabela de Pressão”

A entalpia no estado 1 é igual a entalpia específica de saturação de vapor

Já que o estado 1 está na condição de vapor saturado então a temperatura no estado 1 é igual a temperatura de saturação

Obtendo a temperatura no estado 2 a pressão de e entalpia , da Tabela A-12 “Propriedades de Refrigerante 134a Vapor Superaquecido”, por interpolação entre e

Achando a temperatura do refrigerante no estado 3

Achando o valor da temperatura no estado 3 a pressão de , da Tabela A-11 “Propriedades de Refrigerante 134a Saturado: Tabela de Pressão”

A entalpia no estado 3 é igual a entalpia específica de saturação de vapor

Já que o estado 3 está na condição de líquido saturado então a temperatura no estado 3 é igual a temperatura de saturação

O estado 4 está em condição úmida, então a temperatura no estado 4 é igual a temperatura de saturação a pressão

b) calculando a taxa de vazão mássica do refrigerante

Calculando a potência de entrada do compressor

c) calculando o coeficiente de performance da bomba de calor

d) calculando o coeficiente de performance para a bomba de calor de Carnot

Já que o do ciclo atual é menor que o , essa compressão da bomba de calor é possível.