Um processo necessita de uma transferência de calor de 3 × 106 Btu/h (879,2 kW) a 170°F (76,7°C). Propõe-se que uma bomba de calor por compressão de vapor, trabalhando com Refrigerante 134a, seja utilizada para o desenvolvimento desse processo de aquecimento, utilizando-se uma corrente de água rejeitada a 125°F (51,7°C) como fonte de baixa temperatura. A Fig. 10.39 fornece os dados para este ciclo que opera em regime permanente. A eficiência isentrópica do compressor é de 80%. Esboce o diagrama T–s do ciclo e determine
(a) a entalpia específica na saída do compressor, em Btu/lb.
(b) as temperaturas em cada um dos estados principais, em °F.
(c) a vazão mássica de refrigerante, em lb/h.
(d) a potência do compressor, em Btu/h.
(e) o coeficiente de desempenho e compare com o coeficiente de desempenho para um ciclo de bomba de calor de Carnot operando entre os reservatórios na temperatura do processo e na temperatura das águas rejeitadas, respectivamente.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
Pegando a entropia específica e entalpia específica da Tabela A-11E “Propriedades de R134a Saturado (Líquido-Vapor): Tabela de Pressão” correspondente a pressão de e entalpia
Já que o processo 1-2s é isentrópico, temos que
Passo 3
Calculando a entalpia específica na saída ideal do compressor
Pegando a entropia específica da Tabela A-11E “Propriedades de R134a Saturado (Líquido-Vapor): Tabela de Pressão” correspondente a pressão de no estado saturado
Já que a entropia específica no estado saturado é menor que a entropia específica no estado 2, o vapor no estado 2 está no estado superaquecido.
Então usamos a tabela superaquecido e interpolando. Da tabela A-12E “Propriedades de Vapor de R134a Superaquecido” a pressão de e entropia de
Passo 4
a) Escrevendo a relação para a eficiência do compressor
Passo 5
b) O estado atual na saída do compressor é com pressão e entalpia específica de
Pegando a temperatura no estado 2 atual da Tabela A-12E “Propriedades de Vapor de R134a Superaquecido” a pressão de e entalpia específica de , por interpolação
Passo 6
Pegando a temperatura de saturação da Tabela A-11E “Propriedades de R134a Saturado (Líquid-Vapor): Tabela de Pressão” a pressão de
Passo 7
Pegando a entalpia específica no estado 3, de líquido saturado a pressão de
Pegando a entalpia específica de líquido saturado de R134a a pressão de da Tabela A-11E “Propriedades de R134a Saturado (Líquid-Vapor): Tabela de Pressão”
Já que o processo 3-4 é um processo de estrangulamento,
Passo 8
Considerando o processo 4-1, um processo isobárico com adição de calor
Pegando a temperatura no estado 4 da Tabela A-12E “Propriedades de Vapor de R134a Superaquecido” a pressão de e entalpia específica de , por interpolação
Já que a entalpia específica no estado 4 é maior que a entalpia específica do líquido saturado e menor que a pressão de vapor saturado de , então o estado 4 é uma mistura com temperatura de
Passo 9
c) calculando a taxa de vazão mássica do refrigerante
Passo 10
d) calculando a potência do compressor
Passo 11
e) calculando o coeficiente de performance do ciclo
Calculando o coeficiente de performance da bomba de calor de Carnot (lembrando de converter as temperaturas para a escala Rankine)
Então, o coeficiente de performance do ciclo é menor que o do ciclo de Carnot.
Passo 12
Desenhando o diagrama
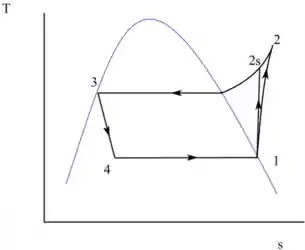
Resposta
a)
b) e e
c)
d)
e) e