Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 10.Problemas - Ex. 42

A Fig. P10.42 mostra esquematicamente um sistema de bomba de calor geotérmica que opera em regime permanente com Refrigerante 22 como fluido de trabalho. A bomba de calor utiliza como fonte térmica água a 55°F (12,8°C) oriunda de poços. Os dados de operação são fornecidos na figura para um dia no qual a temperatura do ar externo é 20°F (–6,7°C). Admita que o compressor opere adiabaticamente. Para a bomba de calor, determine

(a) a vazão volumétrica do ar aquecido para a casa, em ft3/min.

(b) a eficiência isentrópica do compressor.

(c) a potência do compressor, em HP.

(d) o coeficiente de desempenho.

(e) a vazão volumétrica da água dos poços geotérmicos, em gal/min. Para T0 = 20°F, realize um balancete completo da exergia para a potência de acionamento do compressor, e estime e avalie a eficiência da segunda lei para o sistema de bomba de calor.

Passo 1

Saalve, tranquilo?

Vamos resolver juntos mais uma questão de termodinâmica?!

Passo 2

É dado que:

  • Pressão na entrada do compressor: p 1 = 70   l b f / i n 2
  • Temperatura na entrada do compressor: T 1 = 40 ° F
  • Pressão na saída do compressor: p 2 = 180   l b f / i n 2
  • Temperatura na saída do compressor: T 2 = 1 40 ° F
  • Pressão na saída do condensador: p 3 = 180   l b f / i n 2
  • Temperatura na saída do condensador: T 3 = 75 ° F
  • Pressão de expansão na saída da válvula: p 4 = 70   l b f / i n 2

Alguns outros dados importantes:

  • Capacidade da bomba de calor: Q ˙ s a i = 4,2   t o n = 4,2 ⋅ 200 = 840   B t u / m i n
  • Temperatura do ar exterior: T 0 20 ° F
  • Temperatura da água na parede: T e n t , á g u a = 55 ° F = 515 ° R
  • Temperatura de descarga da água: T s a i , á g u a = 45 ° F = 505 ° R
  • Temperatura de retorno da casa: T e n t , a r = 70 ° F = 530 ° R
  • Temperatura de saída da casa: T s a i , a r = 110 ° F = 570 ° R

O diagrama T - s é mostrado abaixo

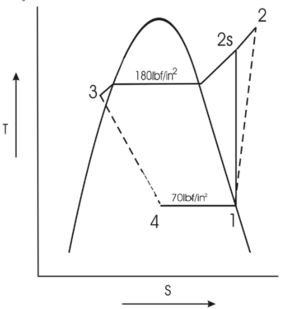
Passo 3

Das tabelas de R-22 superaquecido a p 1 = 70   l b f / i n 2 e T 1 = 40 ° F

h 1 = 109,07   B t u / l b

s 1 = 0,2254   B t u / l b ° R

Das tabelas de R-22 superaquecido a p 2 = 18 0   l b f / i n 2 e T 2 = 1 40 ° F

h 2 = 122,11   B t u / l b

s 2 = 0,2299   B t u / l b ° R

Passo 4

Das tabelas de R-22 saturado a p 3 = 18 0   l b f / i n 2

T s a t = 88,78 ° F

T 3 < T s a t então o estado 3 está na região de sub resfriado

Das tabelas de R-22 saturado a T 3 = 75 ° F

h 3 = h f = 31,79   B t u / l b

s 3 = s f = 0,0661   B t u / l b ⋅ ° R

O processo 3-4 é um processo de estrangulamento, então h 3 = h 4

Passo 5

Das tabelas de R-22 saturado a p 4 = 70   l b f / i n 2

h f = 18,92   B t u / l b

h f g = 88,45   B t u / l b

s f = 0,0414   B t u / l b ⋅ ° R

s g = 0,2219   B t u / l b ⋅ ° R

Já que h 3 = h 4

h 3 = h f + x 4 h f g → 31,79 = 18,92 + x 4 ⋅ 88,45

→ x 4 = 0,1455

E também

s 4 = s f + x 4 s f g = 0,0414 + 0,1455 0,2219 - 0,0414 = 0,06766   B t u / l b ° R

Passo 6

a) a taxa de vazão mássica do ar para a casa é dada por

Q ˙ s a i = m ˙ a r h 2 - h 3 a r = m ˙ a r c p ,   a r T 2 - T 3 a r

→ 840 = m ˙ a r ⋅ 0,24 110 - 70

∴ m ˙ a r = 87,5   l b / m i n

A taxa de fluxo volumétrico de ar aquecido para a casa

p s a i V s a i = m a r R T s a i → 14,7 ⋅ 144 ⋅ V s a i = 87,5 ⋅ 1545 28,97 ⋅ 570

∴ V s a i = 1256,55   f t 3 / m i n

Passo 7

b) A p 2 = 180   l b f / i n 2 e s 1 = s 2 s = 0,2254   B t u / l b ⋅ ° R da tabela de R22 superaquecido

h 2 s = 118,11 + 122,11 - 118,11 0,2254 - 0,2231 0,2299 - 0,2231 = 119,462   B t u / l b

A eficiência do compressor isentrópico

η C = h 1 - h 2 s h 1 - h 2 = 109,07 - 119,402 109,07 - 122,11

∴ η C = 0,7769

Passo 8

c) a potência do compressor

W ˙ C = m ˙ R - 22 h 2 - h 1 = Q ˙ s a i h 2 - h 3 h 2 - h 1 = 840 122,11 - 31,76 122,11 - 109,07

→ W ˙ C = 121,272   B t u / m i n = 7276,32   B t u / h / 2545

∴ W ˙ C = 2,85   h p

Passo 9

d) o coeficiente de performance da bomba de calor

γ = Q ˙ s a i W ˙ C = 840 121,272

∴ γ = 6,9265

Passo 10

e) aplicando o balanço de exergia no evaporador

m ˙ a c p , a T e n t , a - T s a i , a = m ˙ R - 22 h 1 - h 4 → m ˙ a ⋅ 1 55 - 45 = 9,3 109,07 - 31,79

→ m ˙ a = 71,8704   l b / m i n

A taxa de fluxo volumétrico da água

V a g u a = m ˙ a = v a = 71,8704 ⋅ 0,01603 = 1,15208   f t 3 / m i n = 1,15208 / 0,13368   g a l / m i n

∴ V a g u a = 8,61819   g a l / m i n

Passo 11

Contando com a exergia, a potência de entrada do compressor

W ˙ C = m ˙ R - 22 h 2 - h 1 = 9,3 122,11 - 109,07 = 121,272   B t u / m i n

Entrada de exergia da água

E f e n t - E f s a i a = m ˙ a h e n t - h s a i a - s e n t - s s a i a

→ E f e n t - E f s a i a = m ˙ a c p T e n t - T s a i a - T 0 c p ln ⁡ T e n t T s a i - R ln ⁡ p e n t p s a i a

→ E f e n t - E f s a i a = 71,8704 1 ⋅ 55 - 45 - 480 ⋅ 1 ⋅ ln ⁡ 515 505 - 0

∴ E f e n t - E f s a i a = 42,255   B t u / m i n

Passo 12

Destruição de exergia no compressor

E ˙ d C = T 0 σ ˙ C = T 0 m R - 22 ˙ s 2 - s 1 = 480 ⋅ 9,3 0,2299 - 0,2254

∴ E ˙ d C = 20,088   B t u / m i n

Destruição de exergia no evaporador

E ˙ d e v a p = T 0 σ ˙ e v a p = T 0 m ˙ R - 22 s 1 - s 4 + m ˙ a c p w ln ⁡ T s a i T e n t a

→ E ˙ d e v a p = 480 9,3 0,2254 - 0,06766 + 71,8704 ⋅ 1 ⋅ ln ⁡ 505 515

∴ E ˙ d e v a p = 27,696   B t u / m i n

Destruição de exergia no condensador

E ˙ d c o n d = T 0 σ ˙ c o n d = T 0 m ˙ R - 22 s 3 - s 2 + m ˙ a c p w ln ⁡ T s a i T e n t a r

→ E ˙ d c o n d = 480 9,3 0,0661 - 0,2299 + 87,5 ⋅ 0,24 ⋅ ln ⁡ 570 530

∴ E ˙ d c o n d = 2,208   B t u / m i n

Destruição de exergia na valvula

E ˙ d v a l v = T 0 σ ˙ v a l v = T 0 m R - 22 ˙ s 4 - s 3 = 480 ⋅ 9,3 0,06766 - 0,0661

∴ E ˙ d v a l v = 6,9638   B t u / m i n

Passo 13

Exergia entregue ao ar

E f e n t - E f s a i a r = m ˙ a r h e n t - h s a i a r - s e n t - s s a i a r

→ E f e n t - E f s a i a r = m ˙ a r c p T e n t - T s a i a r - T 0 c p ln ⁡ T e n t T s a i - R ln ⁡ p e n t p s a i a r

→ E f e n t - E f s a i a = 87,5 0,24 ⋅ 110 - 70 - 480 ⋅ 0,24 ⋅ ln ⁡ 570 530

∴ E f e n t - E f s a i a = 106,5925   B t u / m i n

Resposta

a) V s a i = 1256,55   f t 3 / m i n

b) η C = 0,7769

c) W ˙ C = 2,85   h p

d) γ = 6,9265

Ver Outros Exercícios desse livro