Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 22
A Fig P.4.22 ilustra um tanque cilíndrico sendo esvaziado através de um duto cuja área de seção transversal é de A velocidade da água na saída varia de acordo com , em que corresponde ao nível da água em m e g é a aceleração da gravidade, dada por . O tanque inicialmente contém 2500 kg de água liquida. Admitindo que a massa específica da água é de , determine o tempo em min em que o tanque contém 900 kg de água.
Passo 1
Desenhe o diagrama de corpo livre para o tanque.
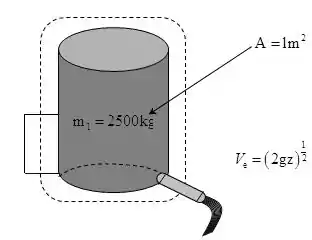
Passo 2
Escreveremos a equação de equilíbrio do fluxo de massa da seguinte forma:
Onde
é a taxa de fluxo de massa da entrada
é a taxa de fluxo de massa de saída
Uma vez que não há água entrando no tanque, portanto
Calcularemos a vazão de massa na saída
é a densidade da água
é a área de saída
é a velocidade na saída
Substituindo
por
por
por .
Passo 3
Calcularemos a altura inicial da água no tanque.
Substituindo
por
por
por
Passo 4
Da equação de balanço de fluxo de massa, teremos:
Substituindo
por
Passo 5
Integraremos as expressões acima para encontrar o tempo para drenar o tanque.
Portanto, o tempo necessário para drenar é de
Resposta
Portanto, o tempo necessário para drenar é de