Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 102
A Fig. P6.102 mostra o diagrama simplificado de uma usina nuclear de potência. A tabela a seguir mostra as vazões e os estados da água em vários pontos do ciclo.
Este ciclo envolve diversos "aquecedores", nos quais calor é transferido dos escoamentos de vapor d'água, que saem das turbinas a determinadas pressões intermediárias, para a água na fase líquida que é bombeada do condensador ao tambor de vapor. A taxa de transferência de calor para a água no reator é igual a
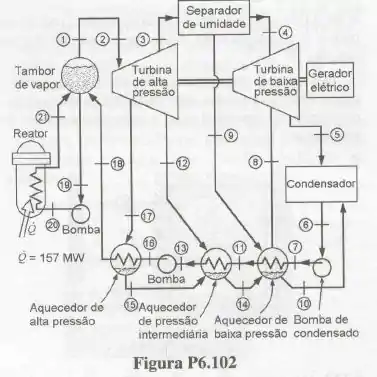
- Admitindo que não haja transferência de calor do separador de umidade, determine a entalpia específica e o título do vapor d’água que entra na turbina de baixa pressão.
- Determine a potência gerada pela turbina de baixa pressão.
- Determine a potência fornecida pela turbina de alta pressão.
- Qual é a razão entre a potência total fornecida pelas duas turbinas e o calor transferido para a água no reator?
Passo 1
Oi pessoal, tudo certo? Vamos analisar essa questão.
No item a, queremos a entalpia específica e o título do vapor d’água que entra na turbina de baixa pressão.
Aplicando o balanço de massa nessa seção, temos que:
Logo:
Aplicando o balanço de energia, temos:
Substituindo os valores, temos:
Da tabela de vapor saturado, temos que este valor está entre vapor e líquido para com:
Logo:
Passo 2
No item b, queremos a potência gerada pela turbina de baixa pressão. Temos que aplicar o equilíbrio de massa na seção da turbina. Temos que:
Substituindo os valores, temos que:
Aplicando a equação de energia para a turbina de baixa pressão, temos que:
Passo 3
No item c, queremos a potência fornecida pela turbina de alta pressão. O principio é semelhante ao do passo anterior. Vamos aplicar o balanço de energia na turbina de alta pressão.
Substituindo os valores, temos:
Para o item d, queremos a relação entre a potencia total de saída das duas turbinas e a potência total fornecida pelo reator: