Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 78

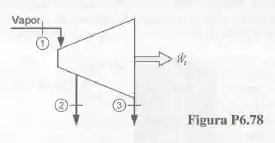
Uma turbina é alimentada com 100 kg/s de vapor d'água a 15 MPa e 600 °C. Num estágio intermediário, onde p = 2 MPa e T = 350 °C, é realizada uma extração de 20 kg/s (ver Fig. P6.78) Na seção final de descarga, a pressão e o título são respectivamente, iguais a 75 kPa e 95. Admitindo que a turbina seja adiabática e que as variações de energia cinética e potencial sejam desprezíveis, determine a potência da turbina.

Passo 1

Opa, tudo bem?

Sabemos que o fluxo de massa que entra deve ser o mesmo que sai, logo:

m ˙ 1 = m ˙ 2 + m ˙ 3

Portanto o fluxo de massa no estado 3 será:

m ˙ 3 = 100 - 20 = 80   k g / s

Analisando os estados propostos no enunciado e casando com as tabelas termodinâmicas, temos que:

h 1 = 3582,3   k J / k g

h 2 = 3137   k J / k g

Para o estado 3 nos foi dado o título, portanto:

h 3 = 384,3 + 0,95 2278,6

h 3 = 2549,1   k J / k g

Sabendo disso, podemos dizer que nossa potência de turbina será:

W T ˙ = m ˙ 1 h 1 - m ˙ 2 h 2 - m ˙ 3 h 3

Calculando encontraremos:

W ˙ T = 91,565   M W

Resposta

W ˙ T = 91,565   M W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Vapor escoa em regime permanente por uma turbina adiabática. Na entrada, o vapor está a 6 Mpa, 400 °C e 80 m/s, e na saída, a 40 kPa, 92% de título e 50 m/s. O fluxo de massa do vapor é de 20 kg/s. De
Ar é expandido por uma turbina a gás adiabática de 500 psia e 800 °F para 60 psia e 250 °F. Considerando a vazão volumétrica na saída correspondente a 50 p é s 3 / s é , a área de entrada equivalente
Um moinho dos anos 1800 utilizava uma roda d’água que tinha 14m de altura; 320l i t r o s por minuto de agua fluiam para a roda próxima ao topo. Quanta potencia, em k W , a roda d’água poderia produzi
Os cataventos diminuem a velocidade do ar fazendo com que este preencha um grande canal a medida que passa através das pas. Considere um cata-vento circular, com um rotor de 7m de diametro em uma velo
Gás dióxido de carbono entra uma válvula de estrangulamento a 5 MPa e 100 °C, saindo a 100 kPa. Determine a variação da temperatura durante esse processo, considerando o CO 2 (a) comoum gás ideal e (b