Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 9.Problemas - Ex. 120
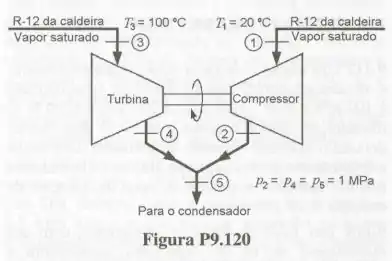
A Fig. P9.120 mostra o esquema de um sistema de refrigeração, essencialmente térmico, onde parte do fluido de trabalho é expandida através de uma turbina para acionar o compressor do ciclo de refrigeração. A turbina produz a potência necessária para acionar o compressor e as correntes de saída se misturam. Especificando claramente as hipóteses utilizadas, determine a relação entre as vazões em massa nas seções 3 e 1 e (, se estiver na região bifásica) se:
a) A turbina e o compressor são reversíveis e adiabáticos;
Passo 1
E aí, tudo bem?
Bora resolver uma questãozinha?
Vai ser rápido e fácil!
Vamos juntos!
Aqui temos que considerar a turbina e o compressor como reversíveis e adiabáticos.
Pela equação de energia, fazendo as devidas considerações, temos:
Para o compressor, temos:
Pela Tabela B.3.1 para , obtemos:
Como o processo é isentrópico:
Na Tabela B.3.2, para essa entropia e pressão de , obtemos:
Substituindo na equação do trabalho do compressor:
Passo 2
Agora, analisando a turbina:
Novamente na Tabela B.3.1, obtemos para :
Temos que:
Devemos calcular utilizando valores da Tabela B.3.1:
Calculando :
Substituindo na equação do trabalho da turbina:
Passo 3
Determine a relação entre as vazões em massa nas seções 3 e 1:
Substituindo os dados:
Assim, completamos uma parte do nosso problema.
Passo 4
Para calcularmos , devemos calcular primeiramente:
Substituindo os dados:
Calculando :
Como não está na região bifásica, não temos como calcular .
Até a próxima questão!