Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 9.Problemas - Ex. 126

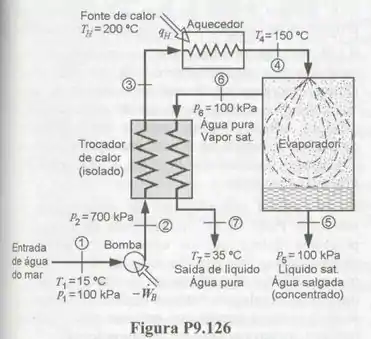
A Fig. P9.126 mostra o esquema de uma instalação utilizada para a produção de água doce a partir de água salgada. As condições de operação da instalação também estão mostradas na figura. Admitindo que as propriedades da água salgada são as mesmas de água pura e que a bomba é adiabática e reversível.

a) Determine a fração mássica de água salgada purificada no processo;

b) Determine w B e q H ;

c) Faça uma análise, utilizando a segunda lei da termodinâmica, da instalação.

Passo 1

Bora resolver esse problema juntos?

Garanto que vai ser bem fácil!

Letra a)

Calculando a fração mássica de água salgada purificada no processo.

Analisando o processo, temos pela equação de energia que:

m ˙ 1 h 4 = m ˙ 1 - m ˙ 7 h 5 + m ˙ 7 h 6

Dividindo por m ˙ 1 :

h 4 = 1 - m ˙ 7 m ˙ 1 h 5 + m ˙ 7 m ˙ 1 h 6

Pela Tabela B.1.1, nós obtemos:

h 4 150 ° C = 632,2   k J / k g

h 5 100   k P a - L í q u i d o   S a t u r a d o = 417,4   k J / k g

h 6 100   k P a - V a p o r   S a t u r a d o = 2675,5   k J / k g

Substituindo na equação:

632,2 = 1 - m ˙ 7 m ˙ 1 ⋅ 417,4 + m ˙ 7 m ˙ 1 ⋅ 2675,5

m ˙ 7 m ˙ 1 = 0,095

Passo 2

Letra b)

Determinando w B e q H .

Considerando um fluxo estacionário e um liquido incompressível, podemos calcular o trabalho da seguinte forma:

w B = - ∫ v d p

w B = - v 1 ( p 2 - p 1 )

Pela Tabela B.1.1:

v 1 15 ° C = 0,001001   m 3 / k g

Substituindo na equação:

w B = - 0,001001 ⋅ 700 - 100

w B = - 0,6   k J / k g

Passo 3

Calculando q H .

Analisando o aquecedor, temos que:

q H = h 4 - h 3

Possuímos h 4 , mas h 3 temos que calcular.

No trocador de calor, temos:

h 2 + m ˙ 7 m ˙ 1 h 6 = h 3 + m ˙ 7 m ˙ 1 h 7

Sabemos que:

w B = h 1 - h 2

Substituindo:

h 1 - w B + m ˙ 7 m ˙ 1 h 6 = h 3 + m ˙ 7 m ˙ 1 h 7

Pela Tabela B.1.1:

h 1 15 ° C = 63,0   k J / k g

h 7 35 ° C = 146,7   k J / k g

Substituindo os dados possuídos:

63 + 0,6 + 0,095 ⋅ 2675,5 = h 3 + 0,095 ⋅ 146,7

h 3 = 303,8   k J / k g

Substituindo na equação de transferência de calor:

q H = 632,2 - 303,8

q H = 328,4   k J / k g

Passo 4

Letra c)

Na última parte da questão, temos que fazer uma análise da instalação utilizando a 2ª Lei da termodinâmica.

Então:

s g e r = - q H T H + 1 - m ˙ 7 m ˙ 1 s 5 + m ˙ 7 m ˙ 1 s 7 - s 1

Dados:

T H = 200 ° C = 473   K

s 1 15 ° C = 0,2245   k J / k g ⋅ K

s 5 100   k P a - L í q u i d o   S a t u r a d o = 1,3068   k J / k g ⋅ K

s 7 35 ° C = 0,5052   k J / k g ⋅ K

Substituindo os dados:

s g e r = - 328,4 473 + 1 - 0,095 ⋅ 1,3068 + 0,095 ⋅ 0,5052 - 0,2245

s g e r = 0,3118   k J / k g ⋅ K

s g e r > 0

A   i n s t a l a ç ã o   a t e n d e   a   2 ª   L e i   d a   T e r m o d i n â m i c a

Viu, falei que ia ser fácil!

Até a próxima!

Resposta

a )   m ˙ 7 m ˙ 1 = 0,095

b )   w B = - 0,6   k J / k g ;   q H = 328,4   k J / k g

c )   s g e r = 0,3118   k J / k g ⋅ K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um suprimento de 5k g / s de amônia a 500k P a e 20 ° C é requerido. Duas fontes estão disponíveis: Uma é líquido saturado a 20° C e a outra é líquido saturado a 500k P a e 140° C . Escoamentos deriva
Em um refrigerador termomecânico, usando amônia como fluido de trabalho, uma turbina com condições de entrada de 2,0M P a e 70 ° C é usada para acionar um compressor que aspira vapor saturado a - 20°
Duas correntes de água, uma de vapor saturado a 0,6M P a , e a outra a 0,6M P a e 600 ° C , são misturadas em um processo adiabático, em regime permanente para produzir uma corrente única a 0,6M P a e
Um compressor é usado para levar vapor d’água saturado de 1M P a para 17,5M P a , com temperatura real de saída de 650° C . Determine o rendimento isoentrópico do compressor e a geração de entropia.
Analise a turbina a vapor descrita no Problema 6.44. Ela é possível?