Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 9.Problemas - Ex. 42
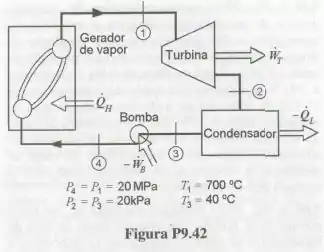
A Fig. P9.42 mostra o esquema de um ciclo motor a vapor d’água que opera a pressão supercrítica. Em primeira aproximação, pode-se admitir que os processos que ocorrem na turbina e na bomba são adiabáticos e reversíveis. Desprezando as variações de energia cinética e potencial, calcule:
a) O trabalho específico realizado na turbina e o estado do vapor na seção de saída da turbina;
b) O trabalho específico utilizado para acionar a bomba e a entalpia do líquido na seção de saída da bomba;
c) O rendimento térmico do ciclo.
Passo 1
Fala galera!
Vamos começar a resolver mais uma questão de termodinâmica, bora lá!
Letra a)
A primeira parte do problema nos pede o trabalho específico realizado na turbina e o estado do vapor na seção de saída da turbina.
Como possuímos a pressão e temperatura de entrada do fluido:
Pela Tabela B.1.3 podemos obter as seguintes propriedades:
Como temos um processo adiabático e reversível, ou seja, isentrópico, assim:
Possuímos a pressão de saída da turbina:
Assim, com algumas propriedades que podem ser obtidas na Tabela B.1.2, podemos calcular o título que saí da turbina:
Então:
Aqui, temos que o estado do vapor na seção de saída da turbina é de vapor saturado.
Passo 2
Agora calculando o trabalho específico realizado na turbina.
Com o título obtidos, e mais algumas propriedades na Tabela B.1.2, podemos calcular a entalpia de saída:
Assim:
Pela equação de energia de um processo adiabático, reversível e que despreza as variações nas energias cinética e potencial, temos:
Vamos seguir para a letra b!
Passo 3
Letra b)
Calculando o trabalho específico utilizado para acionar a bomba.
Pela Tabela B.1.1 analisando a temperatura de entrada na bomba de , obtemos para líquido saturado:
O trabalho da bomba é dado por:
Substituindo os dados:
Calculando a entalpia do líquido na seção de saída da bomba.
Como o trabalho também pode ser expresso por:
Podemos facilmente calcular a entalpia de saída:
Fácil né?
Estamos quase acabando!
Passo 4
Letra c)
Calculando o rendimento térmico do ciclo.
O trabalho do ciclo é dado por:
Abrindo essa equação:
Substituindo os dados:
E assim terminamos, até a próxima!