Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 2.Problemas - Ex. 85
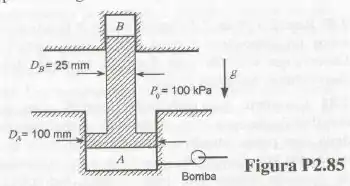
A Fig.P2.85 mostra um pistão especial montado entre as câmaras e . A câmara contém um gás, enquanto que a contém um óleo hidráulico a . Sabendo que a massa do pistão é , calcule a pressão do gás no cilindro .
Passo 1
Vamos lá pessoal! Seguinte temos está situação aqui:
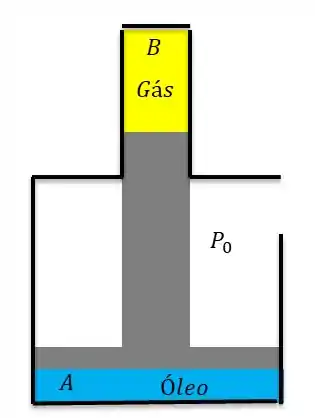
Agora gostaria de lembra de fórmula básica de pressão, que é:
Força dividido pela área.
Agora de uma olhada para este sistema, temos um conjunto de forças atuando nele, e para calcular a pressão no gás, teremos que calcular o balanço de forças nele.
Passo 2
Vem comigo que vamos decompor forcinha por forcinha.
Isolando a força na equação mostrar no passo 1, fica:
Temos pressão do gás que empurra o pistão, logo:
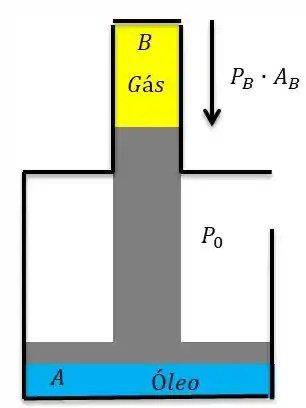
O nosso pistão tem uma massa e tudo que tem massa tem peso, logo:
Como nosso sistema está aberto para atmosfera temos a pressão atmosférica multiplicado a área de contato no nosso óleo.
E nosso óleo reage a isso tudo empurrando para cima:
Passo 3
Somando tudo que aponta para baixo e diminuindo tudo que a ponta para cima o somatório de forças no gás fica:
Calculando as áreas:
Para B:
Isolando , temos:
Substituindo os dados do exercício temos:
A nossa pressão deu negativa. Pois, ao adotamos o referencial da força apontando para baixo como positiva, o que esta tudo bem caso você adotar o referencial de que as forças apontando para baixo são negativas o resultado final ira ser positivo. Mas, o resultado final deverá ser o mesmo.